679 证明题:
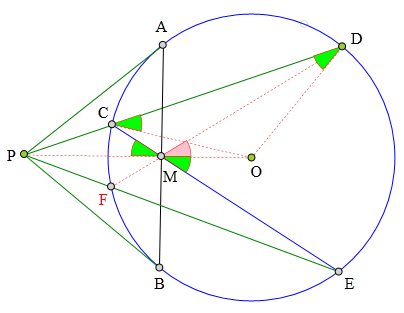
P为⊙O外一点,
PA、PB为⊙O切线,
PCD为⊙O割线,
M为AB中点,
CM交⊙O于E,
求证:
PD=PE
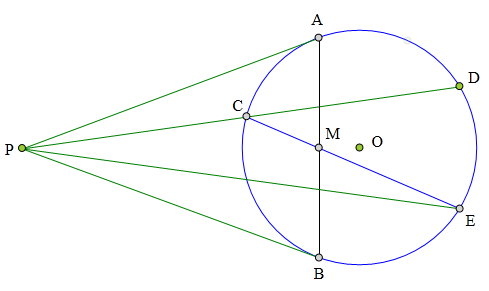
<解法 1:>
取PE与⊙O另一交点F,连接MF,
∵AM为Rt△APO斜边上的高
∴PA²=PC·PD=PM·PO
∴M、O、D、C四点共圆
∴∠PMC=∠PDO=∠DCO=∠DMO
∴∠CMA=∠DMA
同理:∠FMB=∠EMB
∴D、M、F三点工线,
∴∠CMP=∠FMP,
∴△PMC≌△PMF,
∴CM=FM、PC=PF
∴△CMD≌△FMC
∴PD=PE