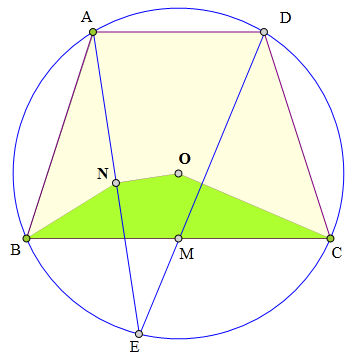
梯形ABCD内接于⊙O，
M为底边BC中点，
DM交⊙O于E，
N为AE中点，
求证：B、N、O、C四点共圆

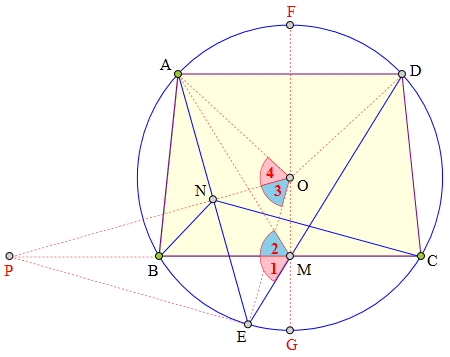
延长OM交⊙O于F、G，
延长ON、CB交于P，
易证：△AMO≌△DMO
∵∠AOF=½∠AOD=∠AED
∴E、M、O、A四点共圆
∴∠EMG=∠OMD=∠OMA=∠OEA=∠OAE
∴∠1=∠2=∠3=∠4（如图)
∴P、E、M、O、A五点共圆
∵PO平分弦AE
∴PO为⊙(PAOE)直径
∴PE丄OE
∴PE²=PN·PO=PB·PC
∴B、N、O、C四点共圆