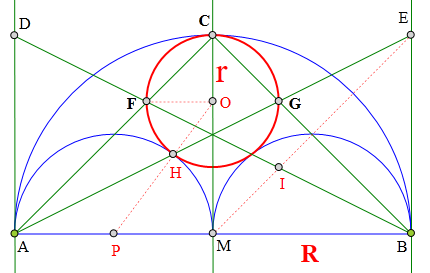
671 证明题:
M为AB中点
分别以AB、AM、BM
为半径的三个半圆在AB同侧
1.作MC丄AB交半圆(AB)于C
2.作AD丄AB,且AD=AM
3.作BE丄AB,且BE=BM
4.连接AC交BD于F
5.连接BC交AE于G
求证:⊙(CFG)与三个半圆都相切
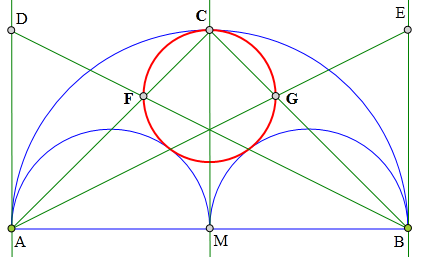
<解法 1:>
取FG中点O,连接FO、ME
取AM中点P,连接PO交半圆P于H
易证AC//ME,F为BD的三等分点
∴O为CM的三等分点,CM=3CO
设CO=r,则MO=2r
PM=PH=½CM=½(3r)
在Rt△POM中有:
PO² = PM² + OM²
∴PO=2.5r,OH=r
即H为⊙O、⊙P的切点,
根据对称性可知⊙O与三个半圆相切