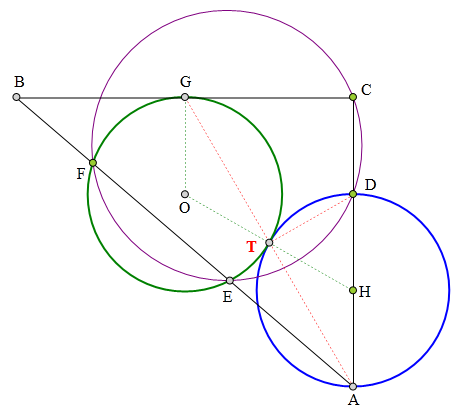
668 证明题:
△ABC中,AC丄BC,
D为AC上一点,
E、F为AB上两点
C、D、E、F四点共圆,
⊙O过EF与BC相切于G,
以AD为直径作⊙H,
求证:
⊙O与⊙H相切

<解法 1:>
连接AG交⊙O于T,
连接DT、OT、HT、OG,
∵C、D、E、F四点共圆
G、T、E、F四点共圆
∴C、D、T、G四点共圆
∵∠C=90°
∴∠DTG=∠DTA=90°
∴T点在⊙H上,即⊙O、⊙H相交于T,
∵OG//AC,∠OGT=∠HAT
∴OTH三点共线
∴T为两圆切点(圆心距为半径之和)