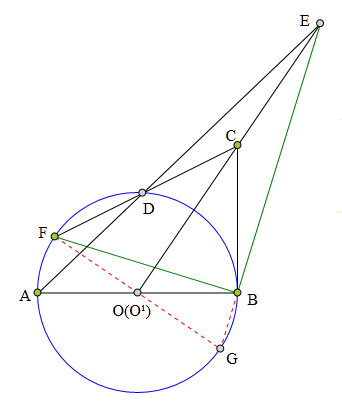
355 证明题:
AB为⊙0直径,
CB切⊙0于B,
D为弧AB上任一点,
CD交⊙0于F,
AD、0C交于点E,
连接EB、FB,
证明:EB丄FB
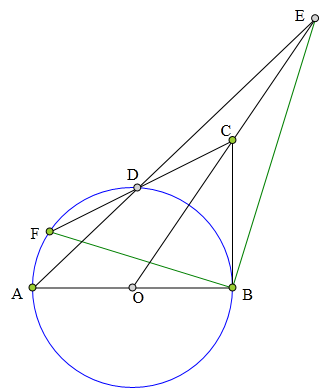
<解法 1:>
过C作CG切⊙0于点G,
连结GA、GB、GC、GD、GE、G0。
易知OC为线段BG的中垂线,
所以EG=EB,∠CEB=∠CEG。
又AG丄BG,所以AG//E0,
所以∠CED=∠DAG=∠DGC,
所以G、D、C、E四点共圆,
所以∠CEG=∠GDF=∠GBF,
所以∠CEB=∠GBF。
而BG丄OE,
所以EB丄FB
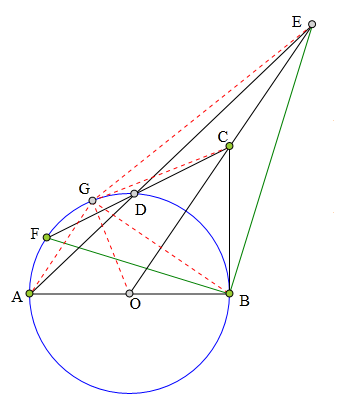
<解法 2:>
延长EB交⊙0于G,
连结GF交AB于0¹。
在六边形FGBBAD中使用帕斯卡定理
知0¹、E、C三点共线,
所以0与点0¹重合为一点。
于是知FB丄EB