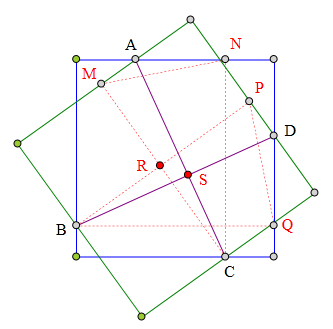
如图：
A、B、C、D为两正方形交点,
求证：AC丄BD

作CM丄HE于M,
作CN丄AD于N,
作BP丄HG于P,
作BQ丄CD于Q。
设AC,BD交于点S,
MC、PB交于点R。
易知CM=BP,CN=BQ,
∠MCN=180°-∠MAN
=180°-∠PDB=∠PBQ,
所以△CMN≌△PBQ,
所以∠DBP=∠DQP
=90°-∠BQP
=90°-∠CNM
=∠ANM=∠ACM,
所以B、C、S、R四点共圆,
所以∠CSB=∠CRB=90°,
即AC丄BD