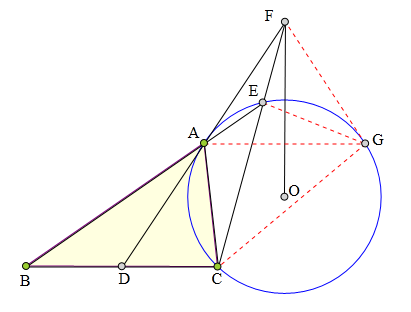
354 证明题:
△ABC中,D为BC中点,
⊙0过A、C两点,
且切DA于A,
延长BA交⊙0于E,
CE延长线交DA于F,
求证:FO丄BC。
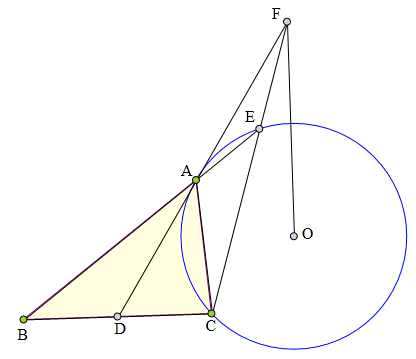
<解法 1:>
延长F0交BC于M。
过0作QN丄EC于N,
则N为CE中点,
连结DN,则DN∥BE。
连结ND、NA、OA,
则OA丄FA。
因为DN//AB,
所以∠NDA=∠BAD=∠EAF=∠NCA,
所以A、D、C、N四点共圆。
又∠0NF=∠OAF=90°,
所以0、N、A、F四点共圆。
于是知∠FOA=∠FNA=∠ADC,所
以A、D、M、0四点共圆,
所以OM丄BC。命题得证
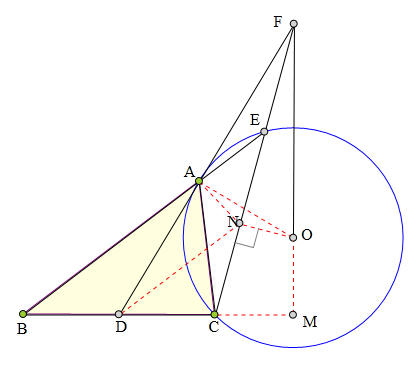
<解法 2:>
作FG切⊙0于G,则FO丄AG。
又因为四边形ACGE为调和四边形,
所以AC、AE、AG、AF为调和线束,
而D为BC中点,
所以 AG//BC。
所以F0丄BC