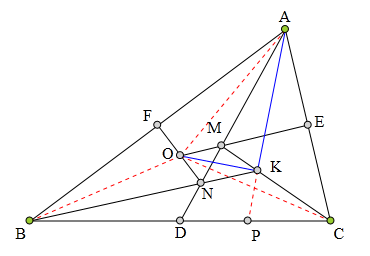
353 证明题:
△ABC中,
D、E、F分别为BC、CA、AB中点,
过E作EM丄AC交AD于M,
过F作FN丄AB交AD于N,
EM、FN交于点0,
CM、BE交于点K,
求证:OK丄AK
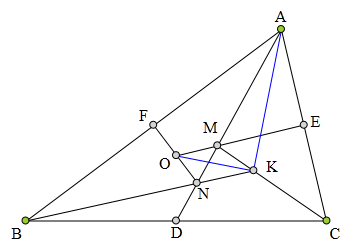
<解法 1:>
连结0A、OB、0C、OD。
延长0K交BC于L,连结AL。
显然点0为△ABC外心,
所以OD丄BC。
根据对称性知∠OCM=∠OAM=∠OBN,
所以B、C、K、0四点共圆,
于是知∠OKB=∠OCB=∠0BL,
所以△0BK∽△OLC,
所以∠0LD=∠OBK=∠0AD,
所以0、D、L、A四点共圆,
所以∠OAL=90°。
另一方面,因为△OBK∽△OLC,
所以OK·0L=0B2=0A²
⇒△OAK∽△OLA
⇒∠OKA=∠OAL=90°
所以OK丄AK。
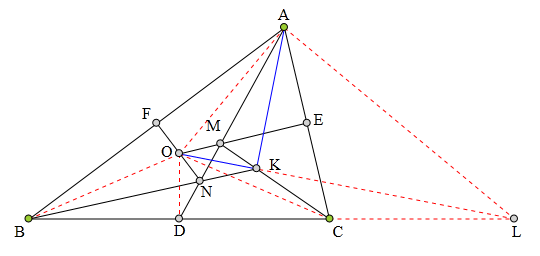
<解法 2:>
记d(P,1)表示点P到直线1的距离。
注意到D为BC中点,
根据对称性知d(A,BK)=d(B,AD)=d(C,AD)=d(A,CK),
所以∠AKB=∠AKC。
如图,延长AK交BC于P,则PK平分∠BKC。
根据条件知0为△ABC外心,
连结0A、0B、0C,
根据对称性知∠0CM=∠OAM=∠0BK,
所以B、0、K、C四点共圆。
所以∠OKM=∠OBC=∠OCB=∠0KB,
即0K平分∠BKM。
所以0K丄AK