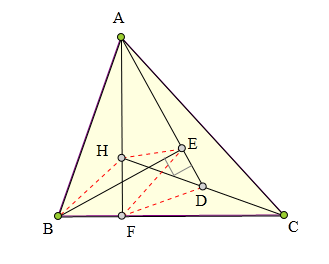
349 证明题:
H为△ABC的垂心,
D为CH中点,
BE丄AD于E,
证明:B、C、E、H四点共圆
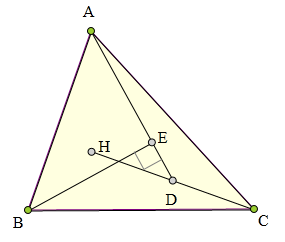
<解法 1:>
延长AD到F,使得DF=DA,
则四边形AHFC为平行四边形,
所以CF//AH, FH//AC。
因为AH丄BC,
所以FC丄BC,
所以B、E、C、F四点共圆;
因为BH丄AC,
所以BH丄FH,
所以B、H、E、F四点共圆,
所以B、H、E、C、F五点共圆,
所以B、C、E、H四点共圆。
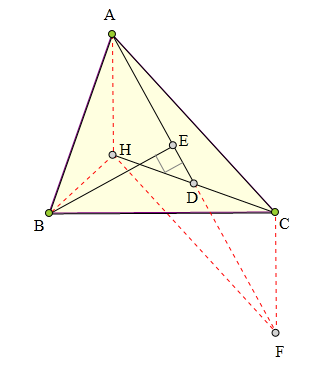
<解法 2:>
延长AH交BC于F,
连结BH、EH、EF、DF。
因为HF丄BC于F,
所以DF=DC=DH,
所以∠DFC=∠DCF=∠HAB。
又显然A、B、F、E四点共圆,
所以∠EFC=∠EAB,
所以∠EFD=∠FAD,
所以DE·DA=DF²=DH²,
所以∠DHE=∠EAH=∠EBC,
所以B、C、E、H四点共圆