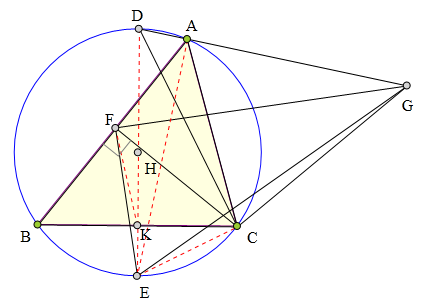
351 证明题:
⊙0为△ABC外接圆,
D为弧BAC中点,
E为弧BC中点,
CF丄AB于F,
连接EF,
过F作FG丄EF交DA延长线于G,
求证:CG=CD。
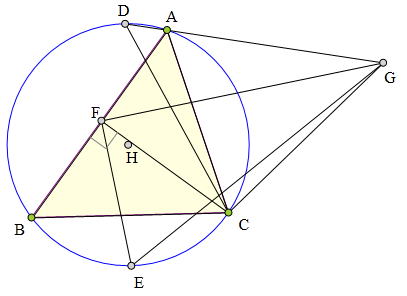
<解法 1:>
连接DE交BC于K,则K为BC中点。
连接FK,知∠BFK=∠FBK。
连接EC、EA,则EA丄DG。
由于FG丄EF,
从而E、F、A、G四点共圆。
于是知∠EGF=∠EAF=∠ECK,
所以△EFG∽△EKC,
所以△ECG∽△EKF,
于是知∠CGE=∠KFE。
从而∠CGD
=∠AGE-∠CGE
=∠BFE-∠KFE
=∠BFK=∠FBK=∠CDG,
所以CG=CD