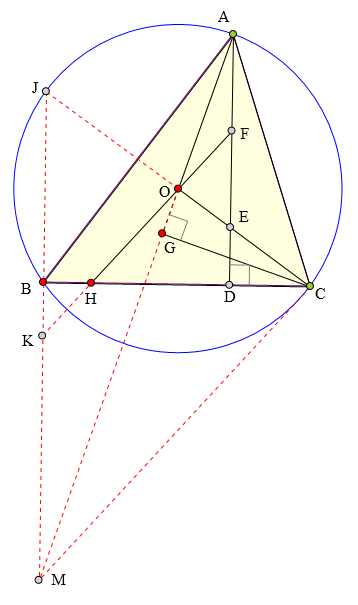
347 证明题:
△ABC内接于⊙0,
AD丄BC于D,
AD交C0于E,
F为AE中点,
FO交BC于H,
CG丄A0于G,
求证:B、H、0、G四点共圆。
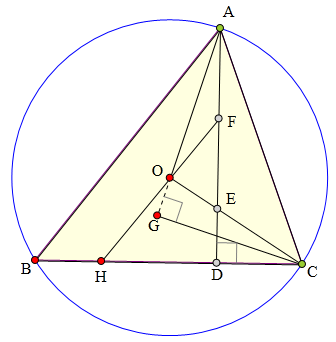
<解法 1:>
延长A0交⊙0于J,
连接EJ、BJ、CJ。
因为∠BCJ=∠BAJ=∠CAE,
∠CBJ=∠CAJ=∠ACE,
所以△BCJ∽△CAE,
所以AE:CJ=AC:BC
⇒AE·BC=AC·CJ=CG·AJ
⇒AE:CG=AJ:BC。
又∠EAJ=∠GCB,
所以△EAJ∽△GEB,
所以∠EJA=∠GBH。
又0F为△AJE中位线,
所以 OF//JD,
所以∠HOJ=∠EJA=∠GBH,
所以B、H、0、G
四点共圆。
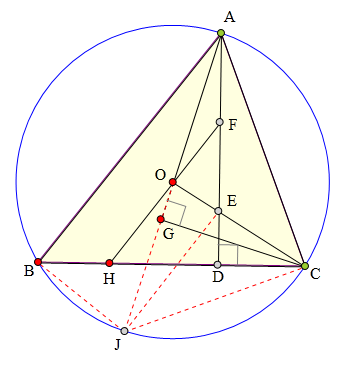
<解法 2:>
延长CG交⊙0于K,则G为CK中点,
且∠KBC=2∠ABC∠EOA。
又易知A、G、D、C四点共圆,
所以∠BCK=∠OAE,
所以△CBK∽△AOE。
又注意到F为AE中点,G为CK中点,
所以△CBG∽△A0F,
故∠CBG=∠AOF,
所以B、H、0、G四点共圆
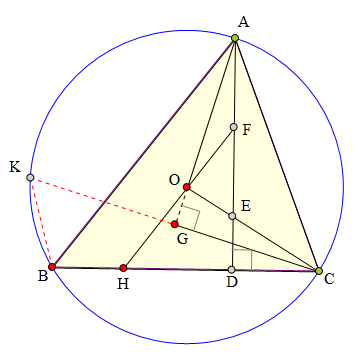
<解法 3:>
延长C0交⊙0于J,
连接JB交A0延长线于M,
连接CM,延长FH交JM于K。
因为JM丄BC,AD丄BC,
所以JM∥AD,
又F为AE中点,
所以K为JM中点,
所以OK为△JMC中位线,
所以0K//MC。
又显然B、M、C、G四点共圆,
所以∠BGO=∠BCM=∠CHO,
所以B、H、0、G四点共圆。