344 证明题:
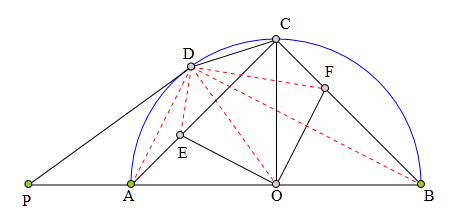
AB为半圆0直径,
0C丄AB,
C在圆上,
P是BA延长线上一点,
PD切⊙0于D,
PE平分∠DPB,
分别交AC、BC于E、F,
求证:∠EOF=90°
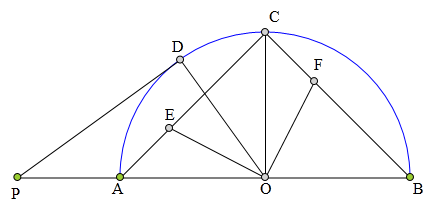
<解法 1:>
连接DA、DB、DC、DE、DF、D0。
则∠DPE
=½∠DPB
=¼(弧BD-弧AD)
=¼[弧BC+弧CD)-(弧AC-弧CD)]
=½弧CD=∠DAE,
所以D、P、A、E四点共圆,
于是知∠PDE=∠EA0=45°=½∠PDO,
所以E为△PDO内心,
所以人0E平分∠AOD。
又∠DBF=∠DAE=∠DPF,
所以D、P、B、F四点共圆,
又PF平分∠DPB,
所以DF=BF,
于是知△FD0≌△FBO,
所以OF平分∠DOB。
所以∠EOF=90°