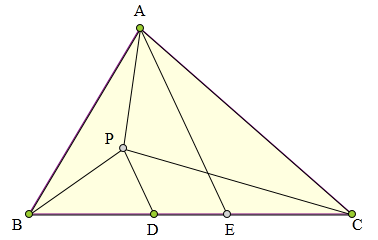
锐角△ABC中,AB且点D和E在边BC上,
满足BD=CE，
若在△ABC内存在点P，
满足PD//AE,
且∠PAB=∠EAC,
证明:∠PBA=∠PCA。

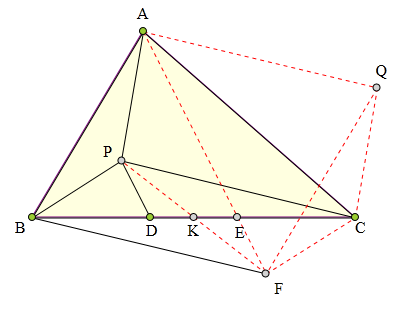
取BC中点为K,则K为DE中点。
延长PK交AE延长线于F,
因为PD//AE,PK=FK,
所以四边形PBFC为平行四边形。
平移△ABP到△QFC,
则四边形APCQ为平行四边形。
因为∠FQC=∠BAP=∠EAC,
所以AFCQ四点共圆,
所以∠ABP=∠QFC=∠QAC=∠ACP。
所以∠PBA=∠PCA。