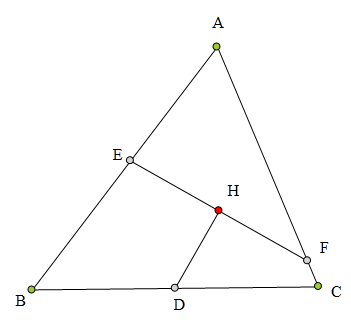
H为△ABC垂心,D为BC中点,
过H作EF丄DH分别交AB、AC于E、F,
求证:H为EF中点。

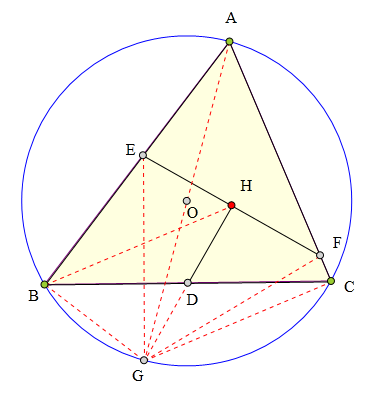
作△ABC的外接圆⊙0,
延长A0交⊙0于G,
连接BH、CH、BG、CG、EG、FG。
因为BG丄AB、CH丄AB,
所以BG//CH。
同理 BH//CG,
所以四边形BGCH是平行四边形，
所以D为GH中点。
又因为B、G、H、E四点共圆,
即为△BGH的外接圆,CE是直径;
G、F、C、H四点共圆,
即为△CHG的外接圆,GF是直径。
而△BGH≌△CHG，
所以GE=GF,
所以H为EF中点。