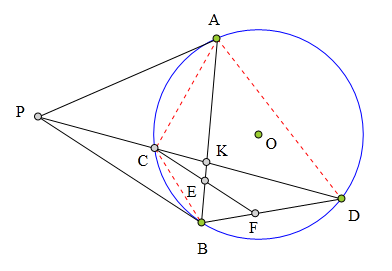
341 证明题:
PA、PB分别切⊙0于A、B,
PCD为⊙0一条割线,
过C作CF∥PB交AB于E,交BD于F,
求证:E为CF中点。
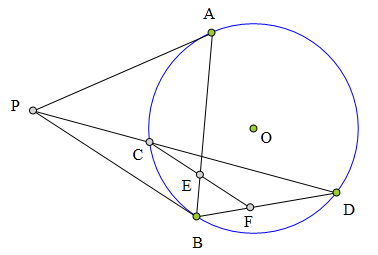
<解法 1:>
设PD、AC交于点K,
作0J丄CD于J,则J为CD中点,
连接EJ。
因为∠0AP=∠0BP=∠OJP,
所以A、P、B、J、0五点共圆,
所以∠JAE=∠DPB∠JCE,
所以A、C、E、J四点共圆,
所以∠CJE=∠CAB=∠CDB,
所以 EJ//BD,
所以E为CF中点
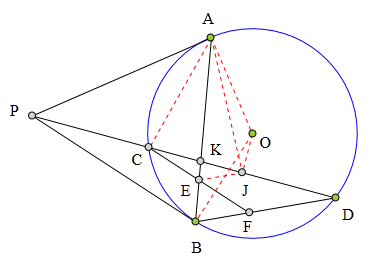
<解法 2:>
因为四边形B、D、A、C是调和四边形,
所以BP、BA、BC、BD是一组调和线束。
因为 CF//PB,
所以E为CF中点