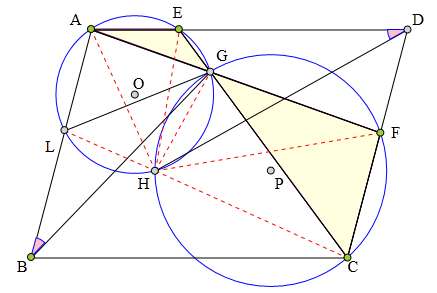
340 证明题:
▱ABCD中,
E、F分别为AD、CD上一点,
AF、CE交于点G,
△AEG的外接圆⊙0
与△CFG的外接圆⊙P交于点H,
连接BG、DH,
求证:∠GBA=∠HDA。
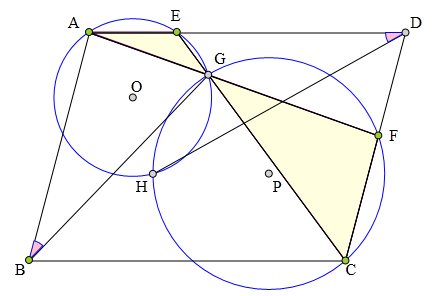
<解法 1:>
连接HG、HE、HA、HF、HC,
则∠HCF=∠HGA=∠HEA,
所以H、C、D、E四点共圆,
同理可知H、F、D、A四点共圆。
延长CH交AB于L,
则∠ALH=180°-∠HCF=∠HGF,
所以A、L、H、G四点共圆,
即L在⊙O上。
连接LG,
则∠LGC
=∠LGH+∠CGH
=∠LAH+∠CFH
=∠LAH+∠DAH
=∠BAD=180°-∠LBC,
所以B、L、G、C四点共圆。
所以∠GBA=∠GCH=∠HAD。
命题得证。