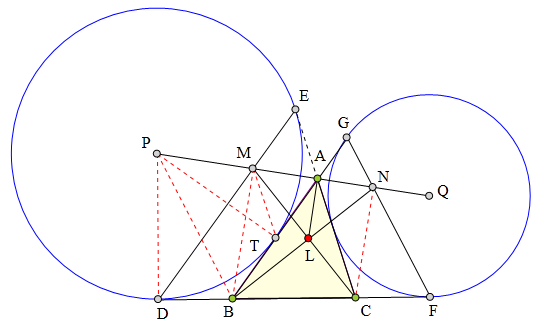
339 证明题:
△ABC中,
旁切圆⊙P分别切CB、CA延长线于D、E,
旁切圆⊙Q分别切BC、BA延长线于F、G,
DE、FG分别交PQ于M、N,
BN、CM交于点L,
求证:AL平分∠BAC。
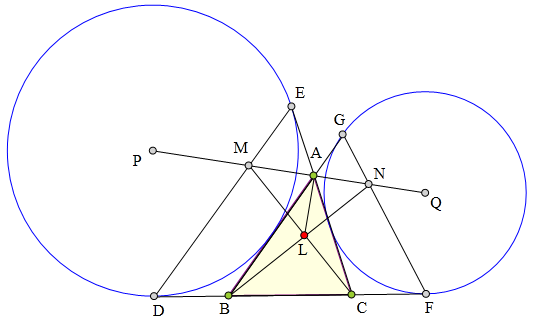
<解法 1:>
设⊙P切AB于T,
则∠PDB=∠PTB=90°,
所以P、D、B、T四点共圆。
又根据对称性知∠MTA=∠MEA=∠BDM,
所以D、B、T、M四点共圆,
所以P、D、B、M四点共圆,
所以BM丄PQ。
同理可知CN丄PQ。
于是知△BAM∽△CAN,
所以AL丄MN,
所以AL平分∠BAC。