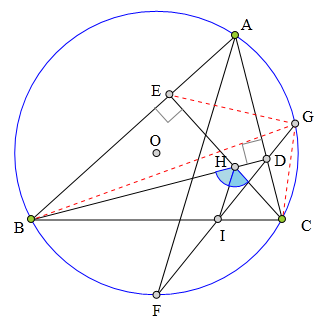
336 证明题:
⊙0为△ABC的外接圆,
AF平分∠BAC交⊙0于F,
H为△ABC的垂心,
CE丄AB于E,
BD丄AC于D,
BD延长线交⊙0于G。
GF交BC于I,
求证:IH平分∠BHC。

<解法 1:>
连结GB、GC、CE。
因为∠GBE=∠GCD,
∠GEB=180°-∠AEG
=180°-∠ADG
=∠GDC,
所以△GEB∽△GDC,
所以CG:CB=CD:BE=CH:BH。
又F为弧BC中点,
所以GI平分∠BGC,
所以CG:CB=CI:BI,
所以CH:BH=CI:BI,
所以IH平分∠BHC。
注:设CE交AF于P,
由以上结论易知∠CHI=½∠BHC
=(180°-∠BAC)
=90°-½∠BAC。
又知∠CPF=∠FAC+∠ACE
=½∠BAC+(90°-∠BAC)
=90°-½∠BAC,
所以∠CHI=∠CPF,
可得IH//AF。