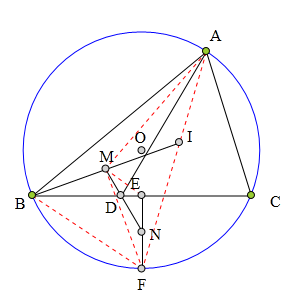
335 证明题:
△ABC内接于⊙0,
E为BC中点,
F为弧BC中点,
I为△ABC内心,
M为BI中点,
N为EF中点,
MN交BC于点D,
证明:DM平分∠ADB。
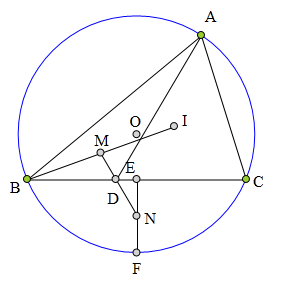
<解法 1:>
连接AF,则I在AF上。
连接BF、MF、ME、MA。
因为∠FIB
=∠BAI+∠ABI
=∠CAI+∠CBI
=∠FBC+∠CBI
=∠FBI,
所以FB=FI。
于是知FM丄BI。
又易知FE丄BC,
所以B、M、E、F四点共圆。
进而知∠EMF=∠CBF=∠IAC=∠IAB,
∠EFM=∠EBI=∠IBA,所以△EMF∽△IAB。
于是知△EMN∽△IAM,
△FMN∽△BAM。
于是知∠DMA=360°-∠FMB-∠FMN-∠BMA
=360°-90°-∠FMN-∠FNM
=90°+(180°-∠FMN-∠FNM)
=90°+∠MFN
=90°+∠MBE
=90°+½∠ABC,
又BM平分∠ABD,
所以点M为△ABD内心,
所以DM平分∠ADB。