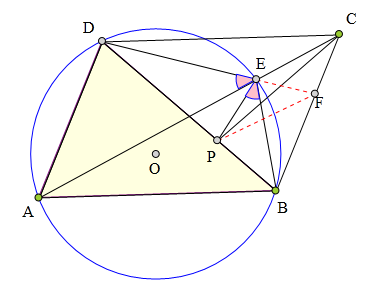
334 证明题:
P是▱ABCD对角线助上一点,
满足∠PCB=∠ACD,
△ABD的外接圆与对角线AC交于点E,
求证:∠AED=∠PEB。
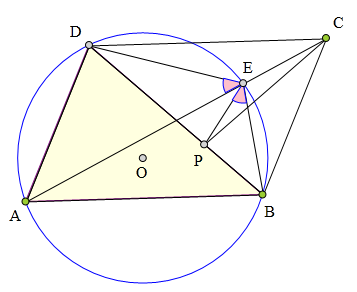
<解法 1:>
根据条件知∠PBC=∠BDA=∠BEA,
∠BCP=∠DCA=∠EAB,
所以△PBC∽△BEA,
所以PB:BE=CB:AE=DA:AE。
又知∠PBE=∠DAE,
所以△PBE∽△DAE,
所以∠AED=∠PEB。
命题得证。
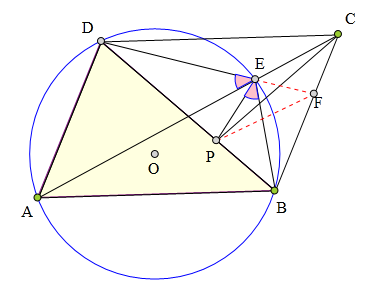
<解法 2:>
延长D交BC于F,连结PF。
因为∠FDP=∠EAB=∠ACD∠FCP,
所以D、P、F、C四点共圆。
于是知∠PFE=∠PCD=∠ACB=∠CAD=∠PBE,
所以P、E、F、B四点共圆。
所以∠PEB=∠PFB=∠BDC=∠ABD=∠AED。
命题得证