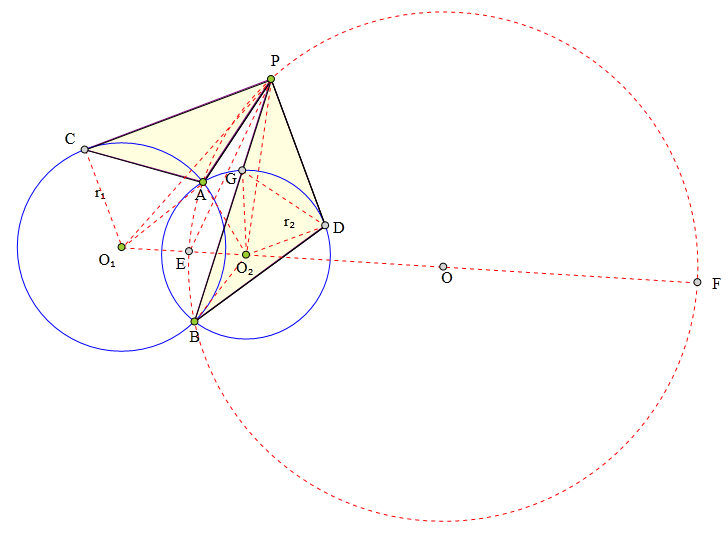
333 证明题:
半径分别为r₁、r₂的两圆交于A、B,
PC分别切两圆于AB异侧于C、D,
PC:PD=r₁:r₂,
求证:△PCA∽△PBD。。
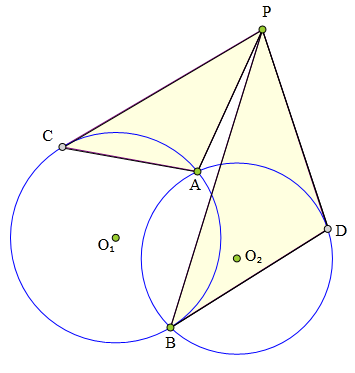
<解法 1:>
连接C0₁、D0₂,
因为PC:PD=C0₁:D0₂,
所以△PCO₁∽△PDO₂.
于是知P0₁:PO₂=C0₁:DO₂=A0₁:GO₂,
所以点P在△O₁O₂A的阿波罗尼斯圆上。
作△O₁O₂A的阿波罗尼斯圆⊙O
交直线O₁O₂于E、F两点,
则知EP平分∠O₁PO₂。
又弧AE=弧BE,
所以EP平分∠APB,
所以∠O₁PA=∠0₂PG。
因为P0₁:PO₂=A0₁:GO₂,
且∠PAO₁与∠PGO₂均为钝角,
根据正弦定理知△0₁PA∽△0₂PG,
所以△PCA∽△PDG∽△PBD。