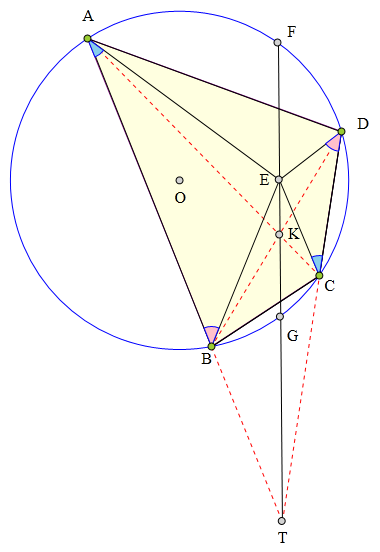
331 证明题:
四边形ABCD内接于⊙0,
E为四边形内一点,
使得∠EAB=∠ECD,∠EBA=∠EDC,
过点E的直线FG平分∠BEC,
交⊙0于F、G两点,
求证: EF=EG。
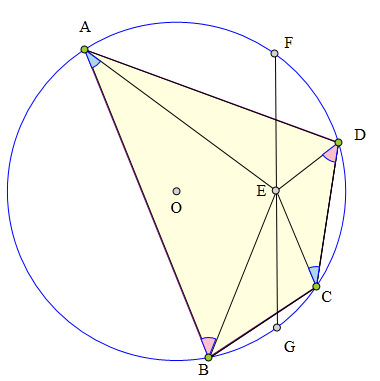
<解法 1:>
连接AC、BD交于点K,
延长AB、DC交于点T。
根据条件知△EAB∽△ECD,
进而知△EAC∽△EBD,
于是知∠EAK=∠EBK,∠ECK=∠EDK,
所以A、B、K、E四点共圆,
C、D、E、K四点共圆,
根据蒙日定理知E、K、T共线。
又因为A、B、K、E四点共圆,
C、D、E、K四点共圆,
所以∠KEB=∠KAB=∠KDC=∠KEC,
所以K在直线FG上,
也即F、E、K、G、T五点共线。
注意到T、K为⊙0的一对共轭点,
故T、K、G、F为一组调和点列。
而TG·TF=TB·TA=TK·TE,
根据调和的性质知,E为FG中点。