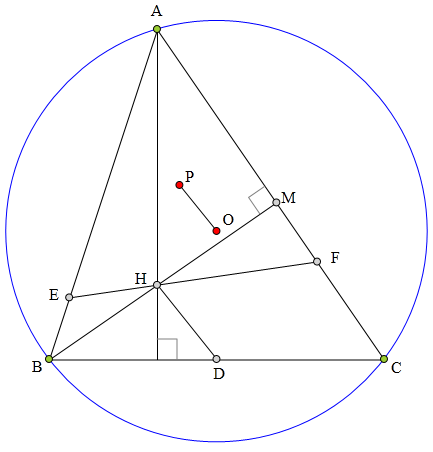
⊙0为△ABC外接圆,
D为BC中点,
H为△ABC为垂心,
E、F分别为AB、AC上一点,
使得AE=AF,
且E、H、F三点共线,
P为△AEF外心,
求证:OP∥HD。

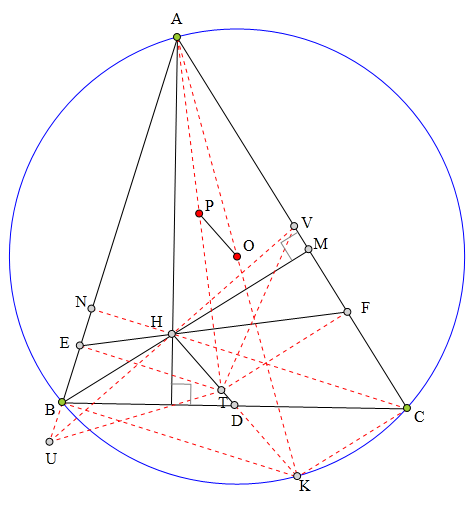
作△ABC外接圆⊙0,
延长AO交⊙0于K,
则四边形BHCK为平行四边形,
故K、D、H共线。
延长BH交AC于M,
延长CH交AB于N,
则B、C、M、N四点共圆,且圆心为D。
过H作DH的垂线分别交AB、AC于U、V,
则根据蝴蝶定理知HU=HV。
延长AP交HD于T,
则AT平分∠BAC,且TU=TV,
故T、U、A、V四点共圆。
根据西姆松定理,
知点T在AU、AV上的垂足与点H共线,
进而知TE丄AU,TF丄AV,
故A、E、T、F四点共圆,且直径为AT,
于是知P为AT中点。
注意到0为AK中点,
故 OP//KT,
从而OK//DH。