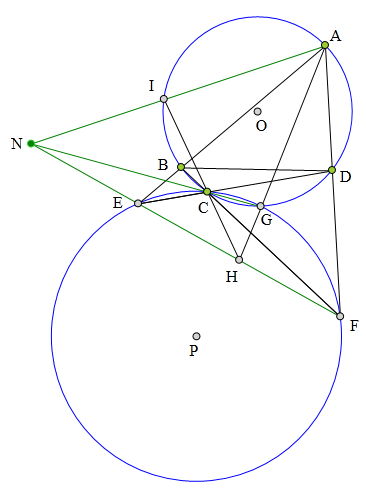
329 证明题:
⊙0的内接四边形ABCD,
AB、DC交于点E,
AD、BC交于点F,
△EFC的外接圆⊙P交⊙0于G,
AG交EF于H,
HC交⊙0于I,
求证:AI、GC、FE三线共点
<解法 1:>
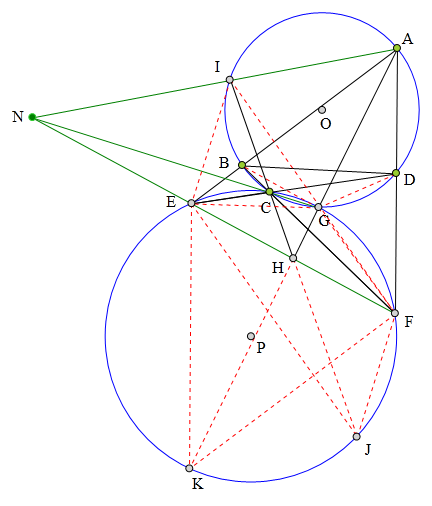
延长AH交⊙P于K,
连接EK、FK、BG、DG、EG、FG。
因为∠GBF=∠GDE,∠GFB=∠GED,
所以△GBF∽△CDE,
所以△GDB∽△GEF。
于是知∠GAD=∠GBD=∠GFE=∠GKE,
所以AF∥EK。
同理可知AE∥FK,
所以四边形AEKF是平行四边形。
所以H为EF和AK中点。
又知CH·JH=GH·KH=GH·AH=CH·IH,
所以H为IJ中点,
所以四边形IEJF是平行四边形,
所以∠EIF=∠EJF=∠EKF=∠EAF,
所以A、I、E、F四点共圆。
根据蒙日定理知,AI、GC、FE三点共线