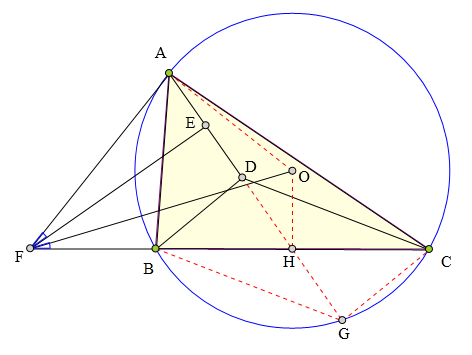
328 证明题:
⊙0为△ABC外接圆,
D为△ABC内一点,使得
∠DAB=∠DBC,
∠DAC=∠DCB,
E为AD中点,
过E作EF丄AD交CB延长线于F,
连接FA、FD、F0,
求证:∠AFD=2∠0FC。

<解法 1:>
延长AD交BC于H,交⊙O于G,
连接BG、CG、OA、0H。
因为∠GBC=GAC=∠DCB,
所以BG∥CD。
同理可知CG//BD,
所以四边形DBGC为平行四边形。
所以H为BC、DG的中点。
又AF²=EF²+EA²
=FH²-EH²+EA²
=FH²-(EH +EA)(EH-EA)
= FH²-AH·GH
=FH²-BH²
=FB·FC,
所以FA切⊙0于A,
所以0A丄FA,
所以0、A、F、H四点共圆,
所以∠FOH=∠FAE,
所以∠OFH=∠AFE,
所以∠AFD=2∠OFC