327 证明题:
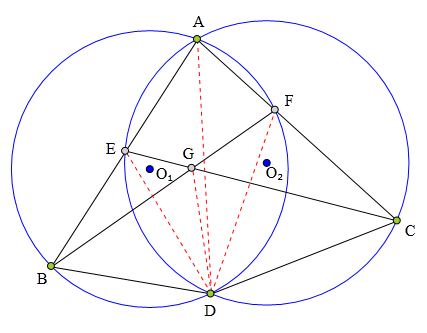
四边形ABCD中,AB=AC,
△ABD外接圆⊙0₁交AC于F,
△ACD外接圆⊙0₂交AB于E,
BF、CE交于点G,
求证: BG:CG=BD:CD
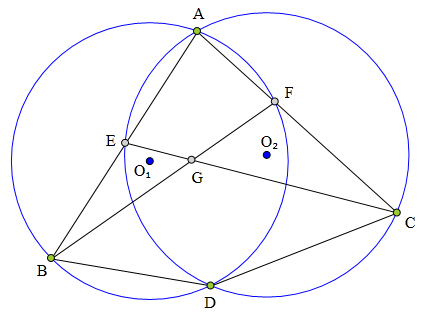
<解法 1:>
连接AD、ED、FD、GD。
因为点D为⊙0₁与⊙0₂的交点,
所以点D为完全四边形AEGFBC的密克点,
所以B、D、G、E四点共圆,
C、D、G、F四点共圆。
所以∠BDG=∠CEA=∠CDA,
∠CDG=∠BFA=∠BDA。
于是知在△BDG和△ADC中,
有∠GBD=∠CAD,∠BDG=∠ADC,
所以△BDG∽△ADC。
同理可知△CDG∽△ADB。
于是知BG:BD=AC:AD=AB:AD=CG:CD,
所以BG:CG=BD:CD。