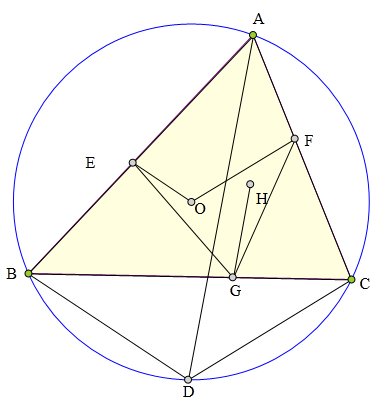
326 证明题:
⊙O为△ABC外接圆,
AD平分∠BAC交⊙0于D,
OE//BD交AB于E,
OF∥CD交AC于F,
H为△ABC垂心,
HG//AD交BC于G,
求证:BE=GE=GF=CF。
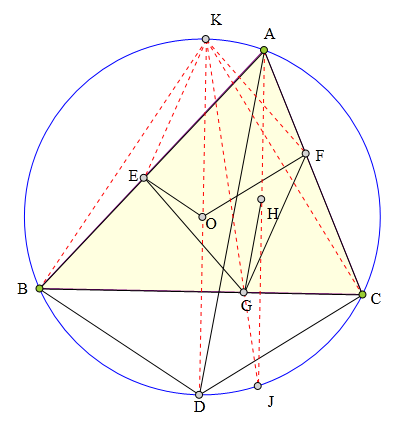
<解法 1:>
延长AH交⊙0于J,则AJ丄BC,
且易知H、J关于BC对称。
延长JG交⊙O于K。
因为∠GJH=∠GHJ=∠DAJ,
所以KD//AJ,
所以KD丄BC,
即DK为⊙0直径,
K为弧BAC中点,
KB=KC。
连接KE、KF。
因为DB丄KB,OE∥BD,
所以0E丄KB,
即直线OE为BK中垂线。
进而知∠KEB
=180°-2∠KBE
=180°-2∠GJH
=2(90°-∠GJH)
=2∠JGC=2∠KGB,
所以E为ΔKBG外心。
同理可知F为△KGC外心。
又根据正弦定理知△KBG和△KCG外接圆半径相等,
所以BE=GE=GF=CF