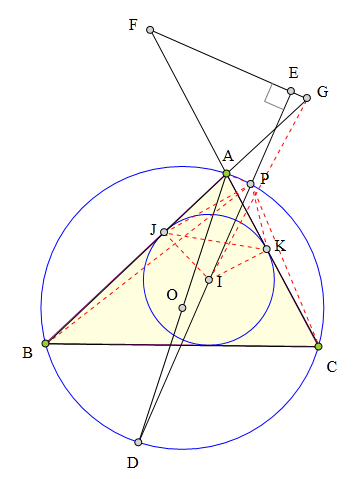
325 证明题:
△ABC内接于⊙0,
内切圆⊙I分别切AB,AC于J、K,
A0交⊙0于D,
连接DI,
延长CA到F,使得AF=BJ,
过F作DI的垂线交DI于E,交BA延长线于G,
求证:AG=CK。
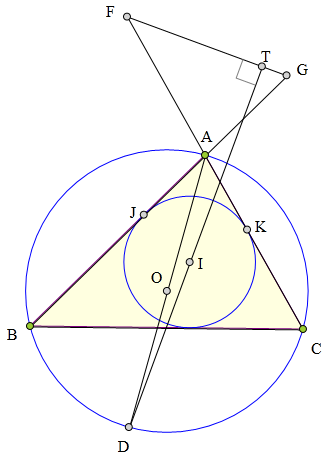
<解法 1:>
设DI交⊙0于P,
则FE丄DE。
连接IJ、IK、JK、PJ、PK、PB、PC,PA,
则AP丄IP。
因为∠AJI=∠AKI=∠API=90°,
所以A、J、I、K、P五点共圆。
所以∠JPK=∠JAK=∠BPC,
于是知∠JPB=∠KPC。又∠PBJ=∠PCK,
所以△PJB∽△PKC,
所以PJ:PK=BJ:CK。
又因为∠FEI=∠FKI=90°,
所以F、E、K、I四点共圆,
所以∠PJK=∠PIK∠AFG,又∠JPK=∠JAK=∠FAG,
所以△PJK∽△AFG,
所以PJ:PK=AF:AG=BJ:CK。
所以AG=CK。