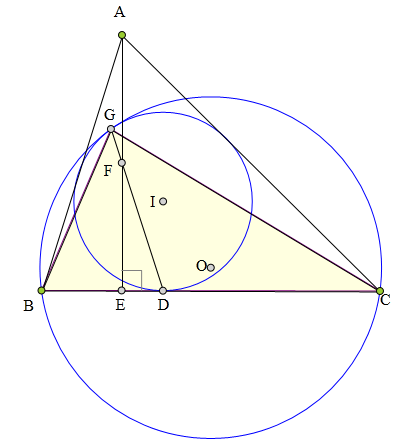
324 证明题:
△ABC内切圆⊙I切BC于D,
AE丄BC于E,
F为AE中点,
DF交⊙I于G,
作△BCG的外接圆⊙0,
求证⊙0、⊙I相切于点G
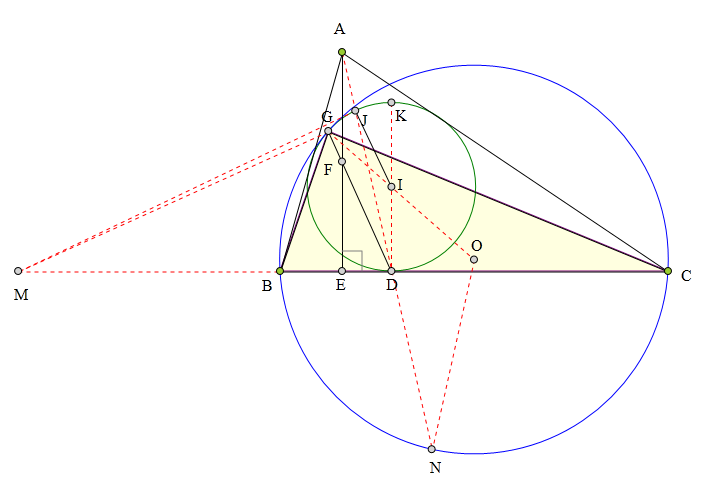
<解法 1:>
连接AD交⊙I于J,
延长DI交⊙I于K,
因为DK//AE,且DG平分AE,
所以DK、DG、DJ、DC是一组调和线束,
所以四边形DKJG是一个调和四边形。
过J作⊙I切线交BC于M,
则M、D、C、B是一组调和点列,
且K、G、M三点共线,
所以DG丄GM,
所以GD平分∠BGC。
延长GD交⊙0于N,
则N为弧BC中点,
所以ON//ID,
所以0、I、G三点共线,
所以⊙0、⊙I相切于点G
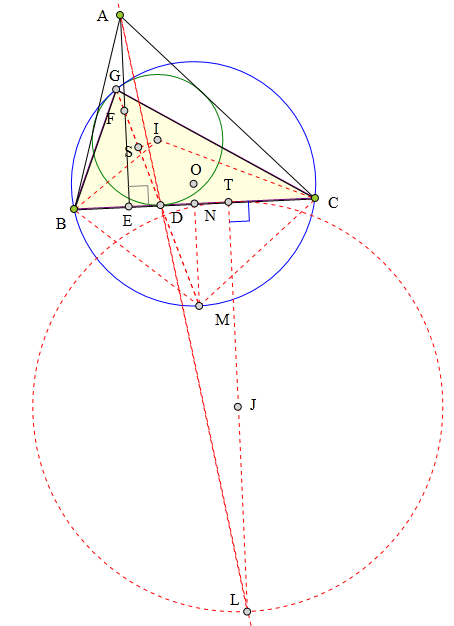
<解法 2:>
作△ABC的A-旁切圆⊙J,
设⊙J切BC于T,则CT=BD。
延长AD交⊙J于L,
根据位似关系知TL为⊙J直径。
注意到J为LT中点,F为AE中点,且LT//AE,
所以J、D、F、G四点共线。
作IS丄GD于S,则S为GD中点。
因为∠ISJ=∠IBJ=∠ICJ,
所以I、S、B、J、C五点共圆。
取DJ中点为M,
则BD·CD=SD·JD=FD·MD,
所以G、B、M、C四点共圆。
作MN丄BC于N,则N为DT中点,
进而知N为BC中点,于是知MB=MC,
故GM平分∠BGC,
从而⊙O、⊙I相切于G