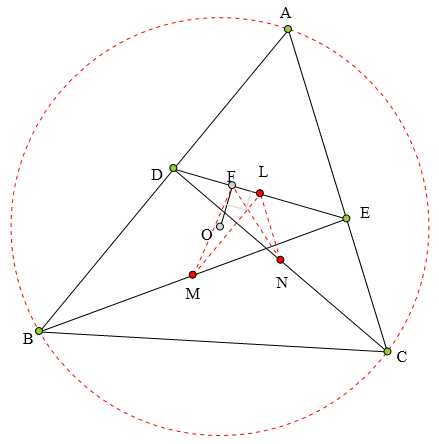
0为△ABC外心,
D、E分别为AB、AC上一点,
OF丄DE于F,
L、M、N分别为DE、BE、CD中点,
求证:F、L、M、N四点共圆

【我们先证明一个引理】
如图,0为△ABC外心，
D、E分别为AB、AC上一点，
OF丄DE于F,
M、分别为BE、CD中点,
则∠MFN=∠A。

【引理的证明】
请参见第381题

【下面借助引理证明原命题】
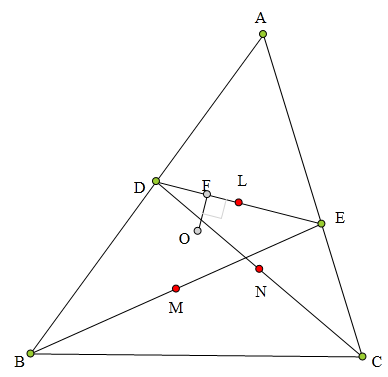
如图,连接MF、NF、ML、NL。
根据引理知∠MFN=∠A。
又因为ML∥BD,NL∥CF,
所以∠MLN=∠A。
所以∠MFN=∠MLN。
所以F、L、M、N四点共圆