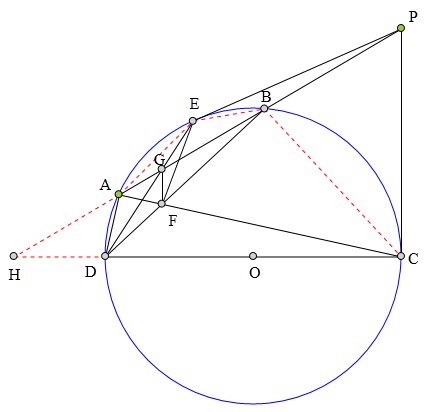
322 证明题:
CD为⊙0直径,
PC、PE分别切⊙0于C、E,
割线PBA交⊙0于A、B,
AC、BD交于点F,
DE交AB于G,
求证:∠GFE=∠ADE
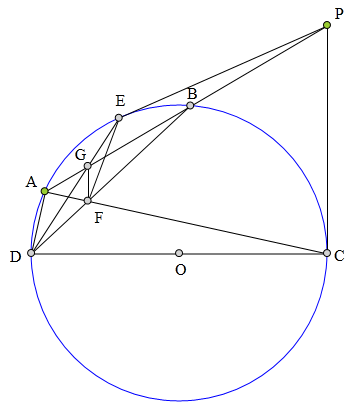
<解法 1:>
延长PA交CD于H,连接AE、BE、BC,
因为四边形AEBC是调和四边形,
所以DA、DB、DE、DC是一组调和线束,
H、G、A、B是一组调和点列,
于是知G在H关于⊙O的极线上。
又F在H关于⊙0的极线上,
所以直线GF是H关于⊙0的极线,
于是知GF丄CD。
从而知∠GFB
=90°-∠FDC=∠DCB
=180°-∠GEB,
所以G、F、B、E四点共圆,
于是知∠GFE=∠GBE=∠ADE