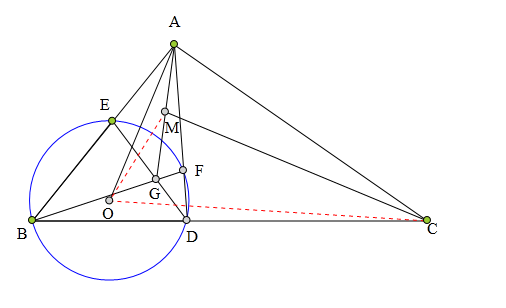
321 证明题:
D是△ABC边BC上一点,
使得∠DAC=∠ABD,
⊙0过点B、D分别交AB、AD于点E、F,
直线EF交DE于点G,
M是AG中点,
求证:CM丄A0。
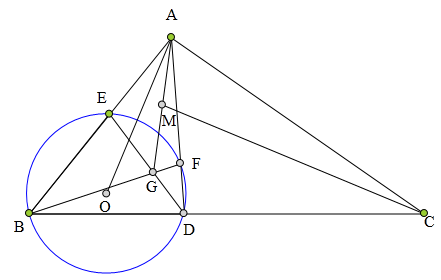
<解法 1:>
连结EF并延长交BC于点J,
延长AG交BD于点I,交EF于H,
连结AJ、GJ,
则知直线GJ为点A关于⊙0的极线,
于是知JG丄A0。
又∠DAC=∠ABD=∠DFJ,
所以HJ//AC,
于是知IH:IA=IJ:IC.
又在完全四边形BDFEJA中,
知AGHI是一组调和点列。又M是AG中点,
所以IG·IA=IH·IM,
即IG:IM=IH:IA=IJ:IC,
于是知CM//JG,
所以CM丄A0
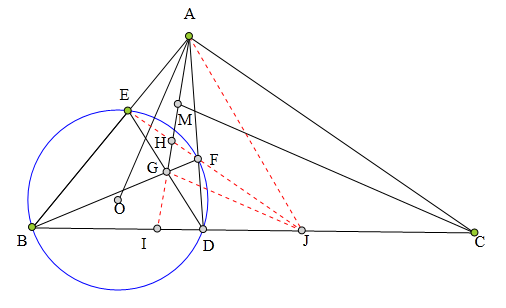
<解法 2:>
因为A、G为一对共轭点,
故M关于⊙0的幂为MA²,
于是知MO²-MA²
=R²
=CO²-CD·CB
=CO²-CA²,
从而CM丄A0!