320 证明题:
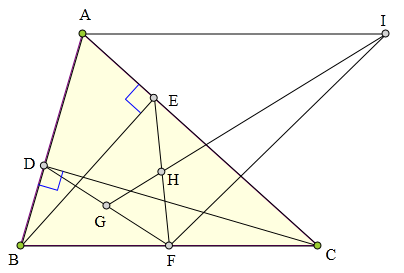
在锐角△ABC中,∠B>∠C,
F是BC的中点,BE、CD是高。
G、H分另是FD、FE的中点,
GH与过A且平行于BC的直线交于I,
求证:AI=FI。
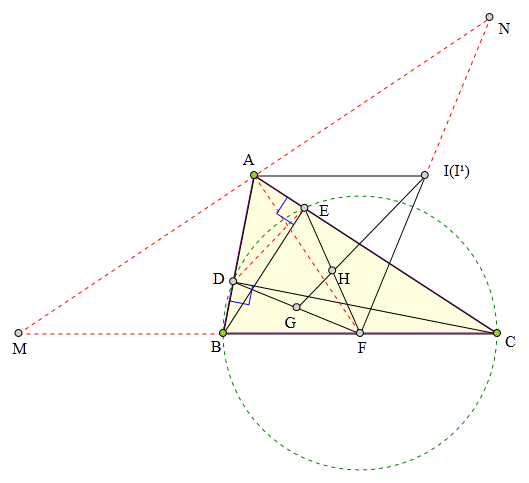
<解法 1:>
连接AF、DE,
显然B、C、E、D四点共圆,且圆心为点F。
过点A作AF的垂线,交CB于M,交DE于N,
根据蝴蝶定理知AM=AN,
从而△AFM≌△AFN,
所以∠AFM=∠AFN。
设GH交FN于I¹,
因为GH//DE,
所以I¹为FN中点,
所以AI¹=FI¹,
所以∠I¹AF∠I¹FA=∠MFA,
所以AI¹∥BC。
于是知I¹与I重合为一点。
所以AI=FI