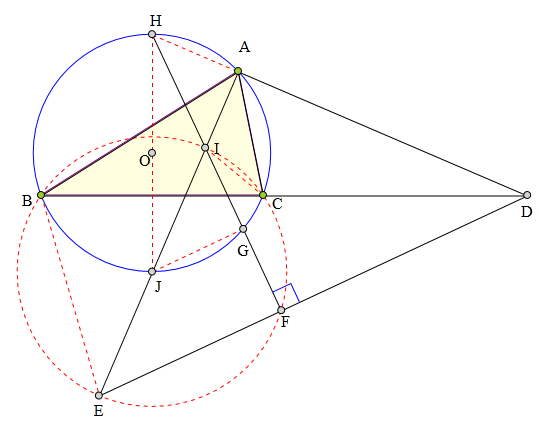
319 证明题:
⊙0为△ABC外接圆,
I、E分别为△ABD的内心和一个旁心,
∠BAC的外角平分线交BC延长线于D,
IF丄DE于F,交⊙0于G,
求证:G为IF中点。
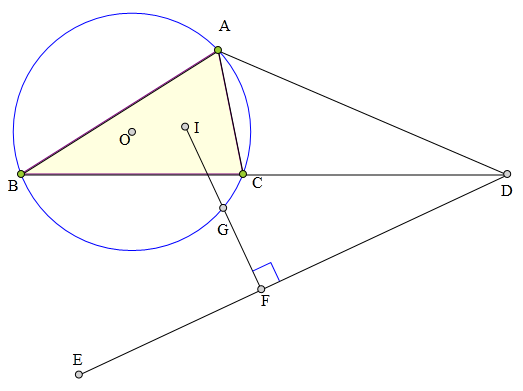
<解法 1:>
连接EB、EC并延长
分别交AD于K、J,易知K、J也是△ABC的
旁心,且△ABC为△EKJ的垂足三角形,
I为△EKJ的垂心,从而⊙0为△EKJ的九点圆。设
⊙0分别交KJ、IE于L、M,
则知L、M分别为KJ和IE的中点。
又易知K、B、C、J四点共
圆,且圆心为L,于是知LI丄DE,
所以L、I、G、F四点共线。
于是知∠MGL=∠MAL=
90°,从而 MG//DE,又M为IE中点,
所以G为IF中点
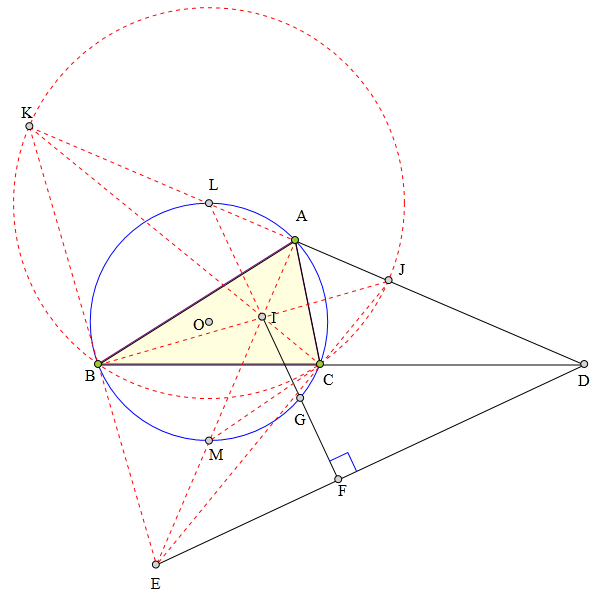
<解法 2:>
连接AE交⊙0于J,则知A、I、J、E共线,且J为IE中点。
又
因为∠IBE=∠ICE=∠IFE,所以B、E、F、C、I五点共圆,且圆心为J。延长DA交⊙0
于H,
则知DF·DE=DC·DB=DA·DH,所以H、A、E、F四点共圆,于是知∠HFE
∠HAE=90°,
所以H、I、G、F四点共线。又∠HGJ=∠HAJ=90°,所以 JG//EF,所以G
为IF中点。