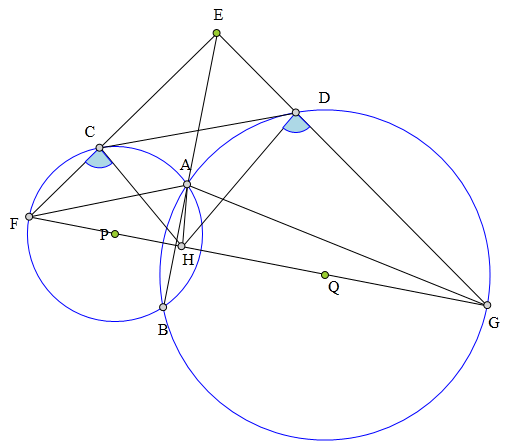
⊙P、⊙Q交于A、B两点,
其外公切线CD分别切两圆于C、D。
E为BA延长线上一点,
EC交⊙P于F,
ED交⊙Q于G,
AH平分∠FAG交FG于H,
求证:∠FCH=∠GDH。

证明:因为E在⊙0、⊙P根轴上,
所以F、C、D、G四点共圆.
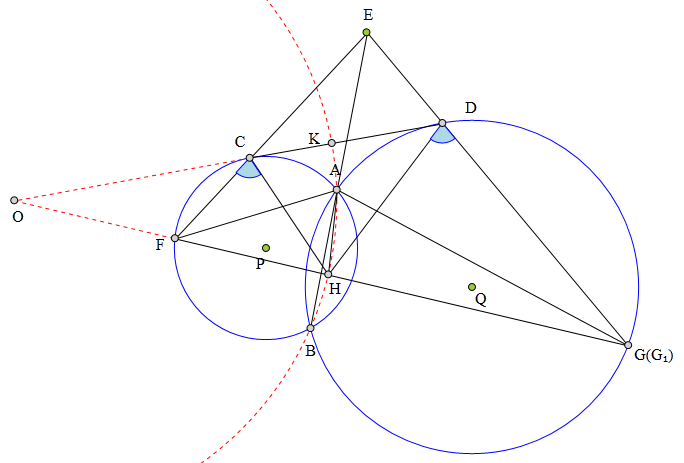
如图,设点0为⊙P、⊙Q的外位似中心,
则⊙P、⊙Q以点0为反演中心互为反形。
延长OF交⊙Q于G₁，则OA²=OC·OD = OF·OG₁，
所以F、C、D、G₁四点共圆。
于是点G₁与点G重合为一点。
以O为圆心，以OA为半径作⊙0交CD于K，
则⊙0为K关于C、D的阿波罗尼斯圆，
由于AH平分∠FAG，
所以点H为⊙0与FG的交点,
从而⊙0也为点H关于F、G的阿波罗尼斯圆。
于是：
∠FCH-∠GDH
=(∠FCA-∠HCA)-(∠GDA-∠HDA)
=(∠FCA-∠GDA)-(∠HCA-∠HDA)
=[(180°-∠FBA)-(180°-∠GBA)]-[(∠HCA-∠HKA)-(∠HDA+∠HKA)+2∠HKA
=(∠GBA-∠FBA)-[(∠KAC-∠KHC)-(∠KAD-∠KHD)+2∠HKA]
=[(∠GBH+∠HBA)-(∠FBH-∠HBA)-2∠HKA
=2∠HBA-2∠HKA=0
所以∠FCH=∠GDH