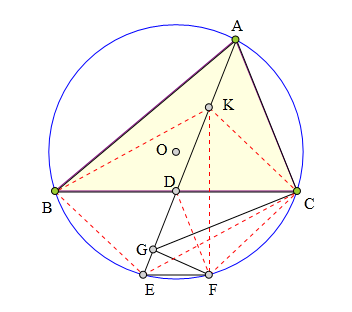
316 证明题:
△ABC内接于⊙0,
D为BC中点,AD交⊙0于E,
过E作EF//BC交⊙0于F,
过C作CG丄AC交AE于G,
求证:∠AGC=∠FGC。
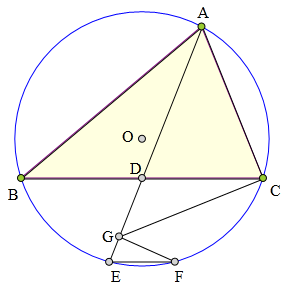
<解法 1:>
连接BE、CF、DF,
过C作CK//BE交AE于K。
因为BD=CD,所以四边形BECK为平行四边形。
于是知CK=BE=CF,∠KCD=∠EBC=∠FCB,
所以△KCD≌△FCD,
所以KF丄BC。
于是知∠CFK=90°-∠FCD
= 90°-∠EBC
= 90°-∠EAC
=∠CGK,
所以G、F、C、K四点共圆。
而CK=CF,
所以∠AGC=∠FGC