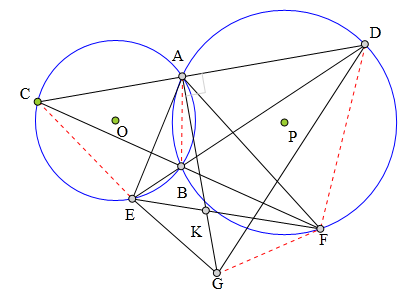
315 证明题:
半径不相等的两圆⊙0、⊙P交于A、B,
过A的直线CD分别交⊙0、⊙P于C、D,
CB延长线交⊙P于F,
DB延长线交⊙0于E,
过A作CD垂线交EF中垂线于G,
求证:AG²=EG²+AC·AD。
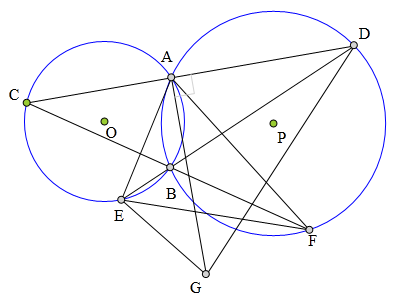
<解法 1:>
连接AB、CE、DF、GF。
因为∠CAE=∠CBE=∠FBD=∠FAD,
∠ACE=∠ABD=∠AFD,
所以△ACE∽△AFD,
所以AC·AD=AE·AF,
又由于⊙0、CP半径不等,
所以AE≠AF。
又因为∠EAG
=90°-∠CAE=90°-∠CBE
=90°-∠FBD
=90°-∠FAD=∠FAG,
GE=GF,
所以A、E、G、F四点共圆。
易知△GEK∽△GAE,
所以EG²=GK·AG。
又易知△AEK∽△AGF,
所以AK·AG=AE·AF=AC·AD。
于是知EG²+AC·AD
= GK·AG + AK·AG
=AG²,
命题得证。