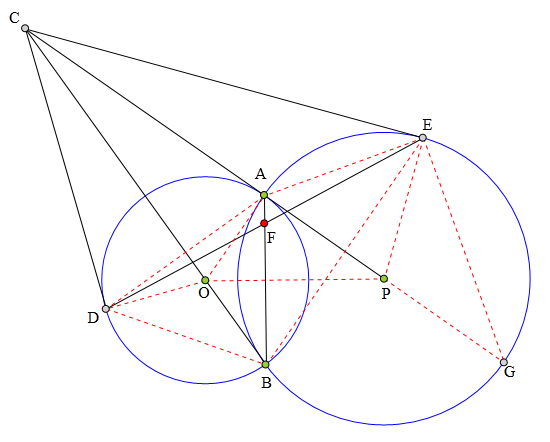
314 证明题:
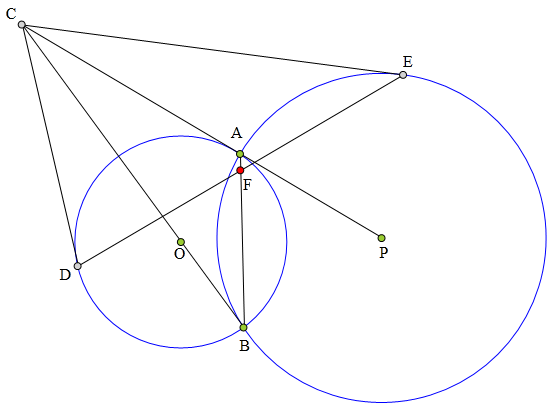
⊙0、⊙P交于A、B两点,
B0、PA延长线交于点C,
CD、CE分别切⊙0、⊙P于D、E,
连接DE交AB于F,
求证:F为DE中点。
<解法 1:>
延长AP交⊙P于G,
连接EG、EP、EA、EB、OP、OA、OD、AD、BD。
设⊙0、⊙P半径分别为r1、r2.
因为CO:CP=sin∠CPO:sin∠COP
=sin∠COP:sin∠BOP
=sin∠APO:sin∠AOP
=AO:AP
=r1:r2,
所以△CDO∽△CEP,于是
知CD:CE=r1:r2.
进而易知△CDB∽△CEG∽△CAE,
于是知DB:AE=CD:CA=CB:CE.
由CD:CA=CB:CE,知△CDA∽△CBE,
从而DA:BE=CA:CE,
于是知 S△DAB:S△EAB
= (DA:BE)·(DB:AE)·(sin∠ADB):(sin∠AEB)
= (CD:CA)·(CA:CE)·(sin∠AOP):(sin∠APO)
= (CD:CE)·(sin∠AOP):(sin∠APO)
= (r1:r2)·(r2:r1)=1.
所有F为DE中点。