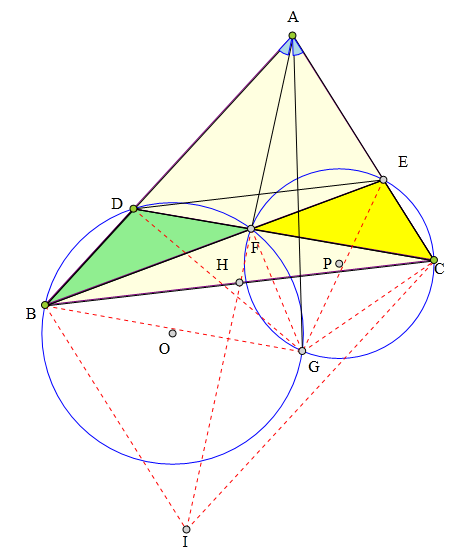
313 证明题:
△ABC中,D、E分别为AB、AC上一点,
且DE//BC,BE、CD交于点F,
△BDF的外接圆⊙0
与△CEF的外接圆⊙P交于点G,
求证:∠BAF=∠CAG。
<解法 1:>
延长AF交BC于H,
因为DE∥BC,
所以H为BC中点,
延长AH到I,使得AH=HI,
连接BC、CI,
则四边形ABIC是平行四边形。
连接GC、GE、GD、GB、FG,
因为∠ACG=∠BFG=∠BDG,
所以A、D、G、C四点共圆。
于是知∠DGC=180°-∠BAC=∠ABI。
同理可知A、B、G、E四点共圆。
所以DBG=∠CEG,∠BDG=∠ECG,
所以△BDG∽△ECG,
所以DG:CG=BD:CE=AB:AC=AB:IB,
所以△DGC∽△ABI,
所以∠BAF=∠GDC=∠CAG。
命题得证。