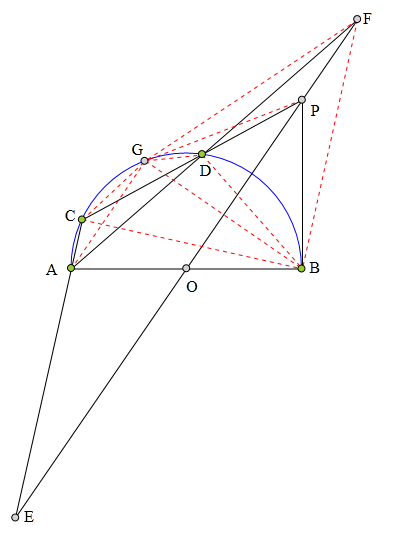
312 证明题:
AB为半圆0直径,
C、D为半圆上两点,
过B作半圆0的切线交CD于P,
直线P0分别交直线CA、AD于E、F,
求证:OE=0F。
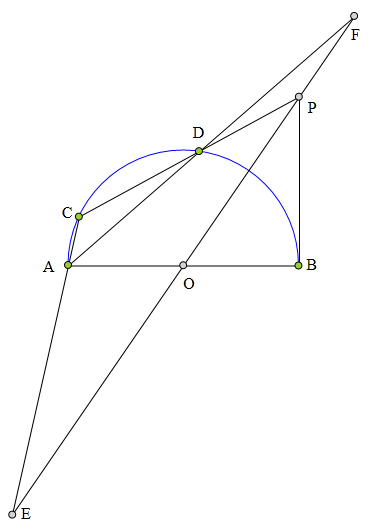
<解法 1:>
过P作PG切半圆0于G,
连接GA、GB、GC、GD、BC、BD。
易知0P丄BG,AG丄BG,所以AG//0P。
又四边形CBDG是调和四边形,
所以AC、AD、AG、AB构成一组调和线束。
又因为AG∥0P,
所以OE=OF。
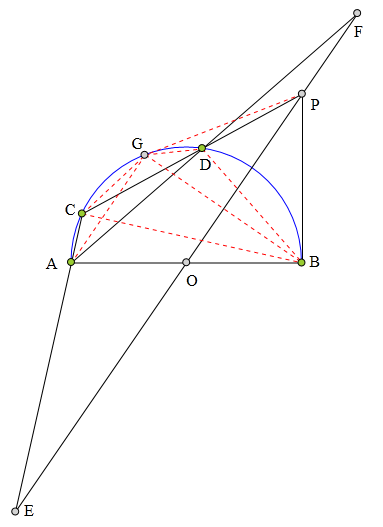
<解法 2:>
作PG切⊙0于G,则B、G关于PO对称,
且P、B、0、G四点共圆,
所以∠GPO=∠GBA=∠GDA,
于是知D、P、F、G四点共圆。
进而知∠FBP=∠FGP∠FDP=∠CDA=∠CBA,
故∠FBC=∠PBA=90°=∠ECB,
所以FB//EA。
而0为AB中
点,
所以OE=OF。