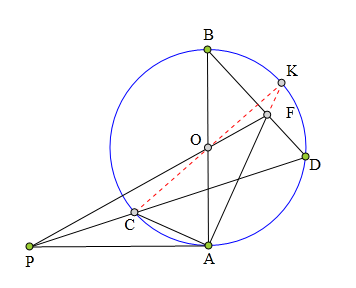
311 证明题:
AB为⊙0直径,
PA切⊙0于A,
PCD为⊙0一条割线,
P0交BD于E,
证明:AC丄AE。
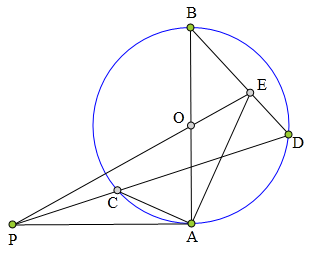
<解法 1:>
作PK切⊙0于K,
则PE丄AK,BK丄AK,
所以 KB//PE。
又注意到四边形CADK为调和四边形,
故BK、BA、BC、BD构成一组调和线束,
从而0为EF中点,
进而知四边形AEBF为平行四边形。
于是知 AE/BC,
故得证
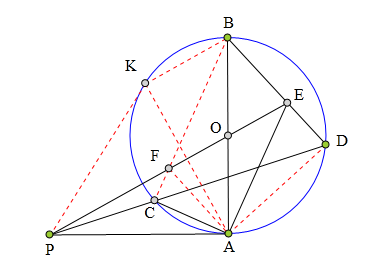
<解法 2:>
连结BC交PE于F。作OK丄CD于K,
则K为CD中点。
注意到0、K、A、P四点共圆,
故∠AKD=∠FOB。
又∠ADK=∠FBO,
故△ADK∽△FBO。
注意点0为AB中点,
故△ADC∽△FBA,
从而知∠FAB=∠ACD=∠ABD,
故 AF//BD,于是知四边形AEBF为平行四边形,
所以AE//BC,
故得证
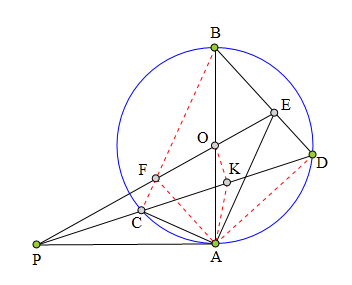
<解法 3:>
延长A交⊙0于K,
在圆内接六边形AABDCK中使用帕斯卡定理,
注意到P、0、E共线,
故C、0、K共线,
故得证