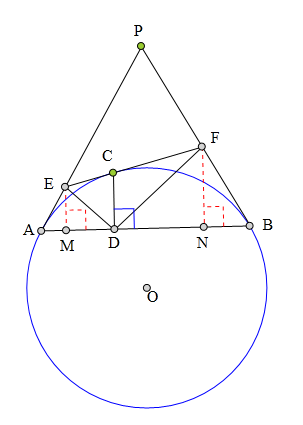
310 证明题:
点P为⊙0外一点,
PA、PB分别切⊙0于A、B,
C为⊙0上一点,
CD丄AB于D,
过C作⊙0的切线分别交PA、PB于E、F,
证明:CD平分∠EDF
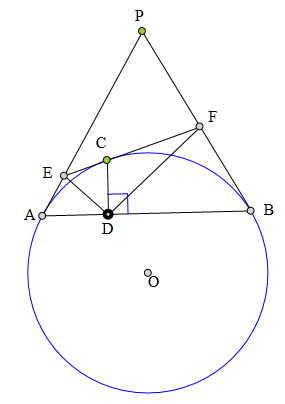
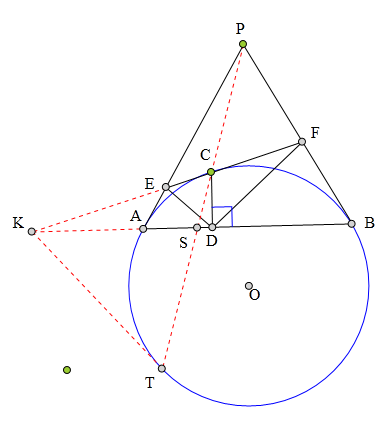
<解法 1:>
延长FE交BA于K,过K作⊙0切线KT切⊙0于T,
注意到点K在P关于⊙0的极线上,
故点P也在点K关于⊙0的极线上,
从而知P、C、T共线。
于是知K、C、E、F构成一组调和点列。
∵CD丄AB,
∴CD平分∠EDF
<解法 2:>
作EM丄AB于M,FN丄AB于N,
则EM:FN=EA:FB=EC:FC=MD:ND,
故△EDM∽△FND,
所以∠EDM=∠FDN,
所以∠EDC=∠FDC