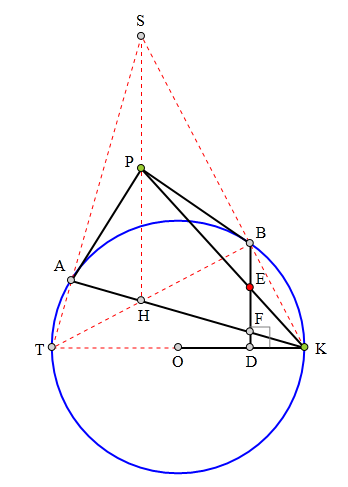
306 证明题:
PA、PB分别切⊙O于A、B,
K为⊙O上一点,
BD丄OK于D,分别交KP、KA于E、F,
证明:E为BF中点.
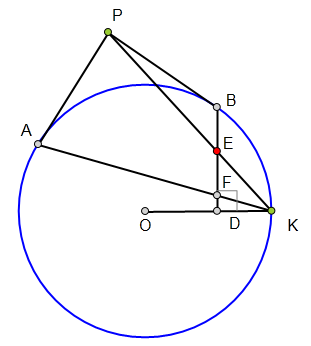
<解法 1:>
过点K作⊙O的切线KT,
则KT//BD.
∵KT、KP、KB、KA构成一组调和线束,
∴故E为BF中点.
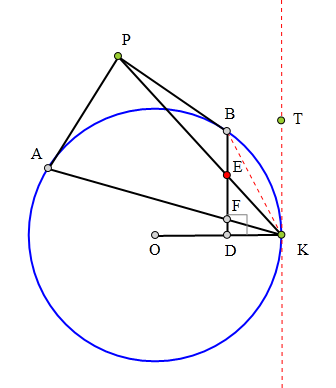
<解法 2:>
延长K0交⊙O于T,
延长TA交KB于S,
连结TB交AK于H,
在圆内接六边形AATBBK中使用帕斯卡定理,
知S、P、H三点共线.
又∵KA丄TS,TB丄KS,
∴点H为△STK垂心.
∴∠SAP=∠TKA=∠ASP,
∴P为SH中点.
∵SH//BD,
∴E为BF中点.