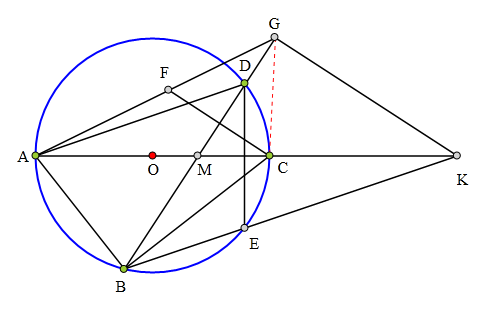
305 证明题:
四边形ABCD内接于⊙O,
且AC为⊙O直径,
D关于AC的对称点为E,
C关于BD的对称点为F,
AF交BD于G, BE交AC于K,
求证:KG丄BG。
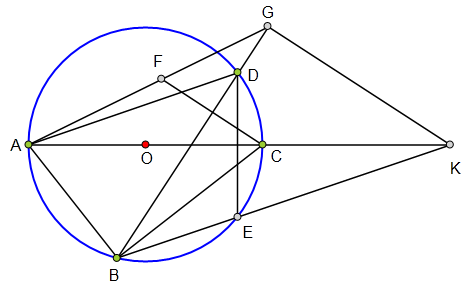
<解法 1:>
根据条件,显然点E在⊙O上,
∴BC平分∠DBE.
设BD交AC于M.
∵∠ABC=90°,
∴AB为∠KBM的外角平分线,
∴KC:MC=KB:MB=KA:MA,
∴AM:CM=AK:CK.
连结GC,根据对称性,GB平分∠AGC,
∴AG:CG=AM:CM=AK:CK,
∴KG为∠AGC的外角平分线,
∴KG丄BG。
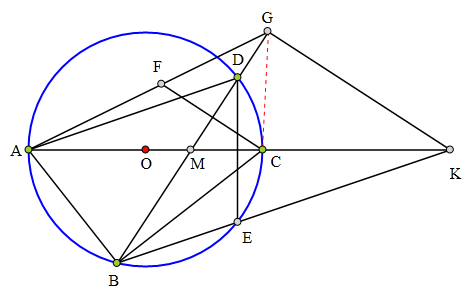
<解法 2:>
∵E为D关于直径的对称点
∴点E在⊙O上,
∴BC平分∠DBE.
设BD交AC于M.
∵∠ABC=90°,
∴K、M、C、A构成一组调和点列。
连结GC,根据对称性,
GB平分∠AGC,
根据调和性质知KG丄BG。