304 证明题:
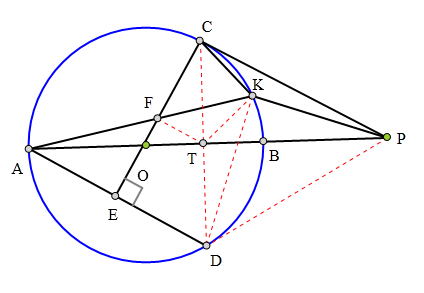
第四题、如图,AB为⊙O直径,
P为AB延长线上一点,PC切⊙O于C,
点C关于AB的对称点为点D,
CE丄AD于E,F为CE中点,
AF交⊙O于K,
求证:AP为△PCK外接圆的切线。
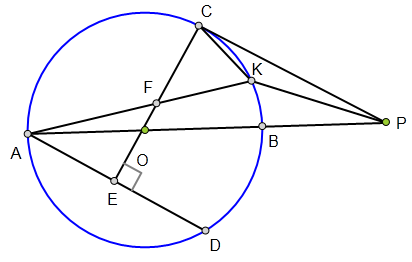
<解法 1:>
连接PD,根据圆的对称性知,
点D在⊙O上,且PD切⊙O于D.
连接CD交AB于T,则CT丄AB,
且T为CD中点.
连结TF、TK。
显然TF为△CDE的中位线,
∴TF//AD,TF丄CE,
且∠TFK=∠DAK=∠TCK,
∴C、F、T、K四点共圆。
∴∠KTP=90°-∠KTC=∠KCD=∠KDP,
∴T、D、P、K四点共圆,
∴∠TPK=∠TDK=∠PCK,
∴AP为△PCK外接圆的切线。