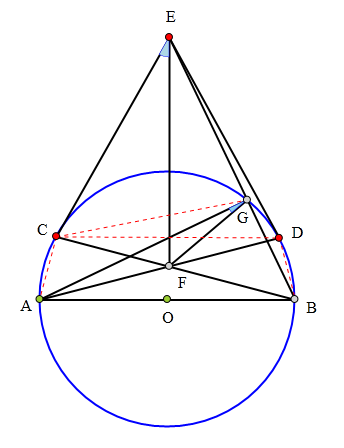
303 证明题:
AB为⊙O直径,
C、D为AB同侧⊙O上两点,
⊙O在C、D两处的切线交于点E,
BC、AD交于点F,EB交⊙O于G,
求证:∠CEF=2∠AGF。
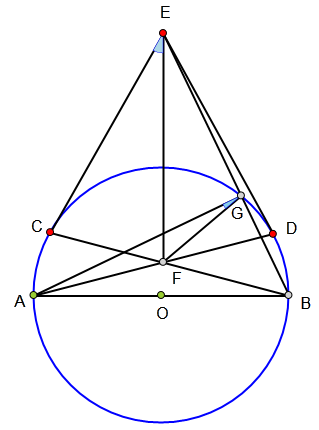
<解法 1:>
连接CG、CD、AC、BD
易知:
∠CFD=½(弧AB+弧CD)
=½[(180°-弧AC)+(180°-弧BD)]
=∠CAB+∠DBA
=∠ECF+∠EDF,
∵EC=ED
∴E为△CFD外心。
∴∠EFC=∠ECF=∠CGE,
∴E、C、F、G四点共圆.
∴∠CGF=∠CEF=2(90°-∠CAB)
=2∠ABC=2∠AGC
∴∠AGF=½∠CGF=½∠CEF
∴∠CEF=2∠AGF