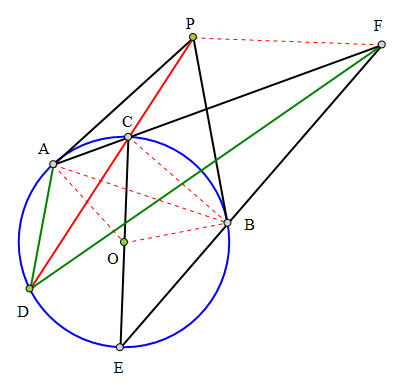
301 证明题:
P为⊙O外一点,
PA、PB分别切⊙O于A、B,
PCD为⊙O一条割线,
CO交⊙O于另一点E,
AC、EB交于点F,
求证:CD平分∠ADF。
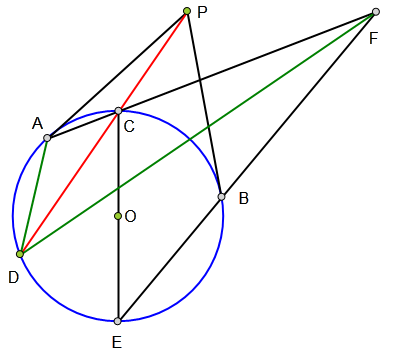
<解法 1:>
延长ED交CA于K,
根据条件知四边形CADB为调和四边形,
∴ED、EC、EA、EB构成一组调和线束,
∴K、C、A、F构成一组调和点列。
∵KD丄CD,
∴CD平分∠ADF。
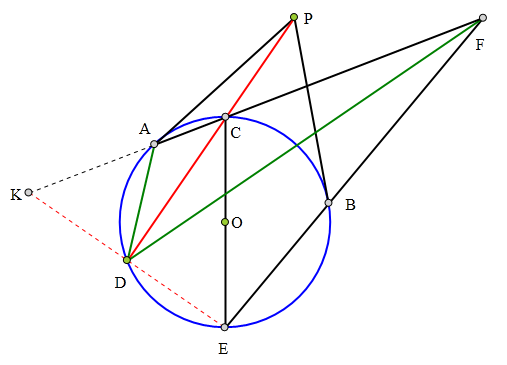
<解法 2:>
连接OA、OB、AB、BC,
∵∠AFB=∠ACE-∠BEC
= ½(∠AOE-∠BOC)
= ½(180°-∠AOC-∠BOC)
= ½∠APB
∵ PA=PB
∴P为△ABF的外心。
∴∠PFA=∠PAC=∠PDA
∴P、A、D、F四点共圆
∴CD平分∠ADF