245 证明题:
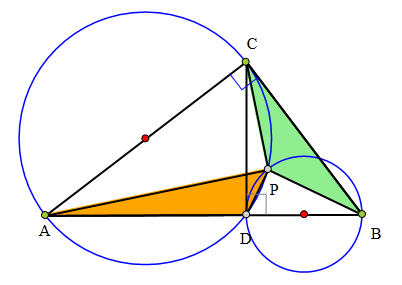
△ABC中,∠ACB = 90°.
CD丄AB于D。
作以AC为直径的圆⊙₁,
和以BD为直径的圆⊙₂,
设⊙₁ 和⊙₂ 在△ABC 内交于P,
求证:S△PAD = S△PBC
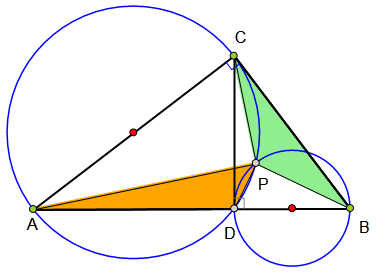
<解法 1:>
由圆周角、弦切角关系,
有∠CAP=∠CDP=∠DBP
∴Rt△APC~Rt△BPD
∴AP·PD= BP·PC
∵∠APC+∠BPD=180°
∴∠APD 和∠CPB 互补
S△PAD=½·AP·PD·sin∠APD
S△PBD=½·BP·PC·sin∠CPB
∴S△PAD = S△PBD