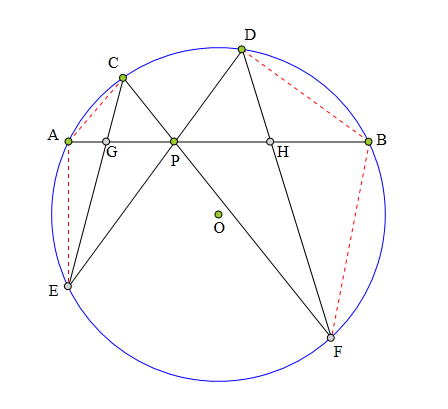
506 证明题:
A、B、C、D是⊙O上的点,
P是弦AB上一点,
弦CE、DF过点P
分别交AB于G、H,
求证:
1/AP-1/BP=1/GP-1/HP
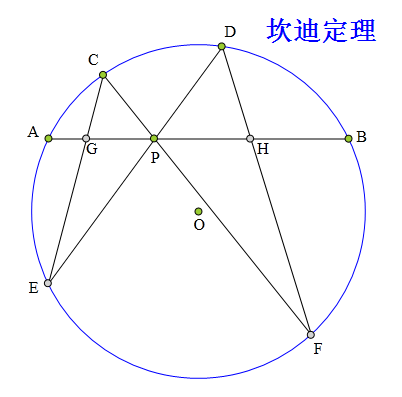
<解法 1:>
连接AC、AE、BE、BF
根据共圆定理得:
S△ACE/S△BDF
=(AC·AE·EC)/(BF·BD·DF)
=(AC/BF)·(AE/BD)·(EC/DF)
=(CE/BP)·(AP/DP)·(EC/DF)
=(CP·EC)/(DP·DF)·(AP/BP)
=(S△CEP/S△DFP)·(AP·BP)
∴(AG/GP)·(PH/HB)
=(S△ACE/S△CEP)·(S△DFP/S△BDF)
=(S△ACE/S△BDF)·(S△DFP/S△CEP)
=(S△CEP/S△DFP)·(AP/BP)·(S△DFP/S△CEP)
=AP/BP
∴(AG/GP)·(PH/HB)=AP/BP
设AP=a,BP=b,GP=x,HP=y
则((a-x)/x)·(y/(b-y))=a/b
∴(a-b)/ab=(x-y)/xy
∴(a/ab)-(b/ab)=(x/xy)-(y/xy)
∴1/a-1/b=1/x-1/y