带括号的四则混合运算计算器（四）

以上课程中我们实现了一个混合表达式的解析和求值过程，效果不太直观，所以这节我们做一个简单的动画来演示整个过程，给课程来个完美收官。

这里有两个过程需要演示，解析过程和求值过程。

先说解析过程，我们已经按解析的顺序把Nodes存入了Calculator的FoundNodes里面，常量和者变量(x)是最底层的Node，所以没有依赖到更底层的Node，其他的Node则依赖于其他的一些Nodes。如果把这种依赖关系画成图，则是一个树形结构，树的根节点就是我们最后解析出来的Node。

树的类型可以根据拥有最大依赖节点数的节点确定，如果只有二元的，则树是二叉树，如果用到了多个参数的函数如(Max(1,2,3))则是多叉树了。不过可以确定，大部分情况下是二叉树，而且很可能不是满二叉树。

下面我们要做的工作就是将树以图形的方式显示出来，这就需要对每个节点计算其位置，然后将父子节点用线连起来，使得显示出来的是一个树形结构，位置的计算逻辑有很多种，为了不麻烦，我们用一种简单的方法——使用满树的结构模式(因为满树是对称的，便于计算排列位置)，然后计算当前树中各个节点在满树中的位置，然后对号入座就OK了。

先来看一下树的定义（具体的实现代码比较长而且逻辑简单，可参考源代码文件），我们还是采用自由布局的控件Canvas来作为Tree和TreeNode的容器：

public class Tree : Canvas
{
                                            double NodeSize = 50;
    public int TreeType { get; private set; }
    private INode RootNode;
    public TextBlock Expression;
    private List<INode> Nodes;//按解析顺序排列的List
}
public class TreeNode: Canvas 
{
                                            public const int ZIndex = 200;
    public INode Node { get; private set; }
    private Tree Tree { get { return Parent as Tree; }}
    public Point Center { get; set; }
    public TextBlock Text;
    public Ellipse Shape;
}

定义很简单，动画也是非常简单的动画，如元素移动或者变色，我们关注的是过程的顺序：

解析的顺序：我们已经存入了FoundList了

求值的顺序：我们在NodeBase中加入一个静态属性CalculatedNodes来记录它，因为GetValue()是递归调用的，我们可以再GetValue() return 之前将Node加入CalculatedNodes列表即可.

public override double GetValue()
{
    var d= 0 - Node.GetValue();
    Record();//将Node加入CalculatedNodes列表
                                                    return d;
}

虽然都是简单的动画，但要写的机械性的代码确实不少，这里我们使用几个通用的重复性事件处理方法来简化编码过程：

//单个元素的连续事件执行，如将Canvas从(0,0)移动到(100,100),
public static void RunCommand<T>(double interval, int times, T obj, 
Action<T> cmd, //主过程
Action<T> startCmd, //初始化过程
Action<T> overCmd//收尾过程
)
{
    var timer = new DispatcherTimer {Interval = TimeSpan.FromMilliseconds(interval)};
    var iTimerCount = times;
    timer.Tick += (s, e) =>
    {
        if (iTimerCount <= 0)
        {
            timer.Stop();
            Run(overCmd, obj);
            return;
        }
        Run(cmd, obj);
        iTimerCount--;
    };
    Run(startCmd, obj);
    timer.Start();
}
//批量元素的连续事件处理，如将10个Canvas依次从(0,0)移动到各自的目标位置,
public static void RunCommand<T>(double interval, List<T> list, 
Action<T> cmd, Action startCmd, Action overCmd)
{
    var timer = new DispatcherTimer { Interval = TimeSpan.FromMilliseconds(interval) };
    int iIndex = 0;
    timer.Tick += (s, e) =>
    {
        if (iIndex >= list.Count)
        {
            timer.Stop();
            Run(overCmd);
            return;
        }
        cmd(list[iIndex++]);
    };
    Run(startCmd);
    Thread.Sleep(100);
    timer.Start();
}

来看看它们的用法：PlayWithShapeMoving()实现了将一个节点从解析的位置移动到它在树中的位置，属于单个元素的重复性事件处理，Play()则实现了对所有节点的动画演示，其中就包含了PlayWithShapeMoving()，而且将PlayWithGetValues()作为“Action overCmd”传入，保证了所有节点都各就各位后才开始求值过程的演示：

//单个节点运动
private void PlayWithShapeMoving(TreeNode shape, Point from, Point to)
{
    const int times = 8;
    double offsetX = (to.X - from.X)/times;
    double offsetY = (to.Y - from.Y)/times;
    EventUtils.RunCommand(100, times, shape,
    s => //动画主过程：重复times次
                                            {
        var p = s.Center();
        s.CenterTo(new Point(p.X + offsetX, p.Y + offsetY));
    },
    s => //初始化过程：
                                            {
        shape.CenterTo(from);//移动到开始位置
        shape.Visibility = Visibility.Visible;
        Expression.Text = shape.Node.Expression;
    },
    s => //收尾动作：画线连接父子节点
                                            s.DrawLinesToChilds());
}
    //动画演示解析和取值过程
public void Play()
{
    var shapes = Children.OfType<TreeNode>().ToList();
    shapes.ForEach(s => s.Visibility = Visibility.Collapsed);
    var startPosition = Expression.Center();
    var shapeList = //根据解析顺序排序Shapes
    Nodes.Select(node => shapes.FirstOrDefault(n => n.Node == node)).ToList();
    EventUtils.RunCommand(1000, shapeList,
    s => PlayWithShapeMoving(s, startPosition, s.Center), //动画演示解析过程
                                            null, //初始化（无）
    PlayWithGetValues //动画演示取值过程
                                            );
}

来看看运行截图：

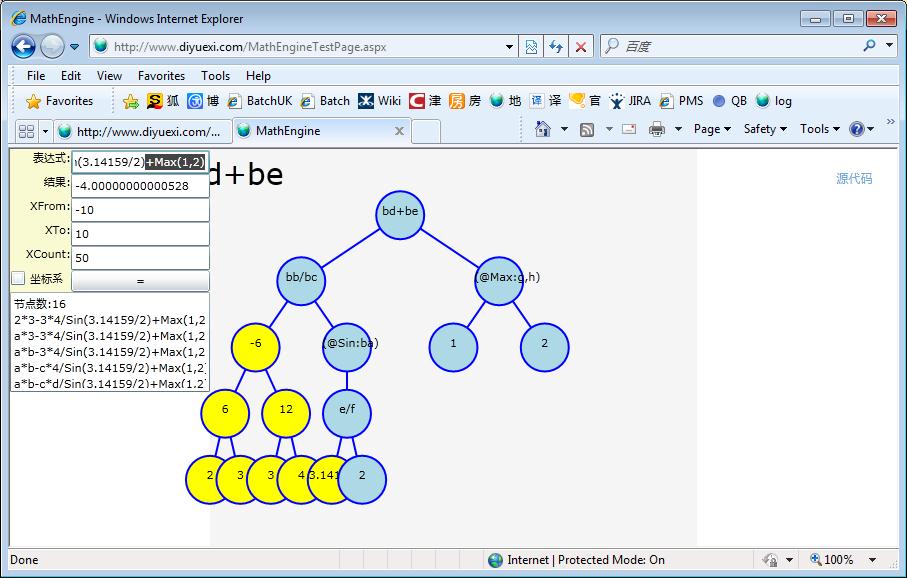
表达式的解析就到此为止了，虽然我们还有很多事情没有做，例如对变量有效区间的计算、非法表达式的检测、性能测试等等…，这是都是很重要需要完善的地方，以后会根据需要加以完善！

下一部分我们将开启新的功能模块——实现几何作图功能，因为涉及到UI编程就会和很多的事件打交道，几何作图也不是一篇就能讲清楚的！下一节我们就从简单的尺规作图三大元素之一的“点”开始，然后从点到线从线到面，来探索我们奥妙无穷的几何宇宙！

数学编程

第二部分：编程技能的简单应用

带括号的四则混合运算计算器（四）